【答案】
分析:解法一:(1)利用二次函數根的分布的知識進行轉化,得到參數a的方程組或不等式組,求解方程或解不等式.
(2)求出f(0)•f(1)-f(0)的關于參數a的表達式,然后利用(1)中解出的a的取值范圍,求出f(0)•f(1)-f(0)的取值范圍,與
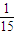
比較.
解法二:基本與解一同,在對第二問大小的比較上,求出用了作差法,(1)中求出的是值域,用函數值的最大值與之比較.
解法三:第一小題中用的是根系關系轉化為關于參數a的不等式,然后解不等式,第二題中通過根與系數的關系構造不等式,利用基本不等式求解.
解答:解:法1:(Ⅰ)令g(x)=f(x)-x=x
2+(a-1)x+a,
則由題意可得
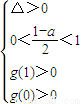
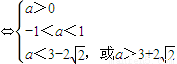
.
故所求實數a的取值范圍是
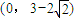
.
(II)f(0)•f(1)-f(0)=2a
2,令h(a)=2a
2.
∵當a>0時,h(a)單調增加,
∴當

時,
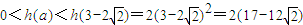
=
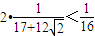
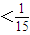
即
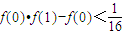
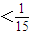
.
法2:(I)同解法1.
(II)∵f(0)f(1)-f(0)=2a
2,由(I)知
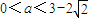
,
∴
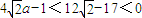
.又
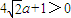
,于是
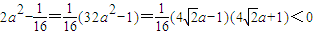
,
即
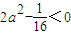
,故
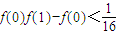
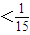
.
法3:(I)方程f(x)-x=0?x
2+(a-1)x+a=0,由韋達定理得x
1+x
2=1-a,x
1x
2=a,于是
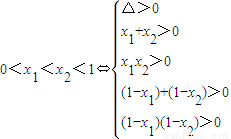
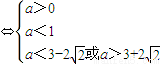
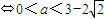
.
故所求實數a的取值范圍是
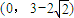
.
(II)依題意可設g(x)=(x-x
1)(x-x
2),則由0<x
1<x
2<1,
得f(0)f(1)-f(0)=g(0)g(1)=x
1x
2(1-x
1)(1-x
2)=[x
1(1-x
1)][x
2(1-x
2)]
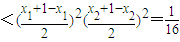
,故
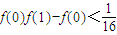
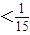
.
點評:本小題主要考查二次函數、二次方程的基本性質及二次不等式的解法,考查推理和運算能力.

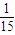 的大小,并說明理由.
的大小,并說明理由.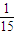 比較.
比較.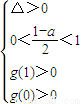
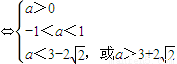 .
.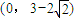 .
. 時,
時,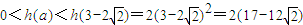 =
=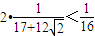
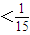
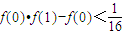
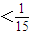 .
.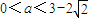 ,
,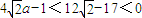 .又
.又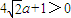 ,于是
,于是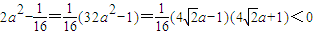 ,
,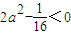 ,故
,故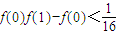
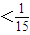 .
.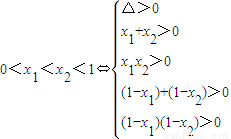
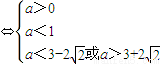
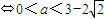 .
.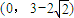 .
.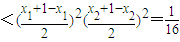 ,故
,故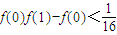
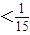 .
.
