已知函數f(x)=x2-ax-aln(x-1)(a∈R)
(1)當a=1時,求函數f(x)的最值;
(2)求函數f(x)的單調區間.
解:(1)函數f(x)=x
2-ax-aln(x-1)(a∈R)的定義域是(1,+∞)
當a=1時,f(x)=x
2-x-ln(x-1),
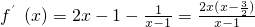
,
當x∈

時,f
′(x)<0,
所以f (x)在

為減函數.
當x∈
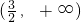
時,f
′(x)>0,
所以f (x)在
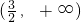
為增函數,
則當x=

時,f(x)有極小值,也就是最小值.
所以函數f (x)的最小值為
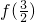
=
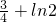
.
(2)
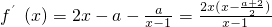
,
若a≤0時,則
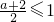
,f(x)=
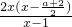
>0在(1,+∞)恒成立,
所以f(x)的增區間為(1,+∞).
若a>0,則
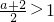
,故當
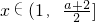
,f′(x)=
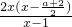
≤0,
當
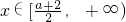
時,f(x)=
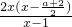
≥0,
所以a>0時f(x)的減區間為
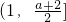
,f(x)的增區間為
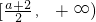
.
分析:(1)首先求出函數的定義域,把a=1代入函數解析式后,求出函數的導函數,由導函數等于0求出函數的極值點,結合定義域可得函數在定義域內取得最值的情況,從而求出函數的最值.
(2)把原函數求導后,對參數a進行分類,根據a的不同取值得到導函數在不同區間內的符號,從而得到原函數的單調區間.
點評:本題考查了利用導數研究函數的最值,求函數在閉區間[a,b]上的最大值與最小值是通過比較函數在(a,b)內所有極值與端點函數f(a),f(b) 比較而得到的.考查了利用導數研究函數的單調性,函數的導函數在(a,b)內恒大于等于0,原函數在該區間內單調遞增,函數的導函數在(a,b)內恒小于等于0,原函數在該區間內單調遞減,此題是中檔題.

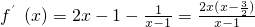 ,
, 時,f′(x)<0,
時,f′(x)<0, 為減函數.
為減函數.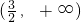 時,f′(x)>0,
時,f′(x)>0,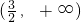 為增函數,
為增函數, 時,f(x)有極小值,也就是最小值.
時,f(x)有極小值,也就是最小值.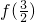 =
=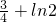 .
.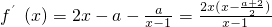 ,
,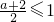 ,f(x)=
,f(x)=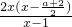 >0在(1,+∞)恒成立,
>0在(1,+∞)恒成立,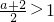 ,故當
,故當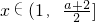 ,f′(x)=
,f′(x)=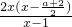 ≤0,
≤0,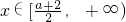 時,f(x)=
時,f(x)=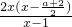 ≥0,
≥0,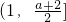 ,f(x)的增區間為
,f(x)的增區間為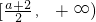 .
.

 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案 新思維寒假作業系列答案
新思維寒假作業系列答案 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<