
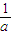 <
< ;
;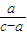 >
>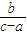 .
.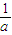 >
>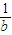 ,故命題①錯誤;
,故命題①錯誤; >0,又a>b>0,
>0,又a>b>0,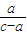 >
> ,故命題④也是正確的.
,故命題④也是正確的.

科目:高中數學 來源: 題型:
| a |
| b |
| c |
| b |
| c |
| d |
| a |
| b |
| c |
| d |
| a |
| a |
| MP |
| MA |
| MB |
| OP |
| OA |
| OB |
| OC |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| b |
| a |
| b |
| c |
| c• |
| b |
| a |
| b |
| c |
| BA |
| BM |
| BN |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| 2 |
| 5 |
| 2 |
| π |
| 8 |
| 5 |
| 4 |
查看答案和解析>>
科目:高中數學 來源:福建省三明一中2012屆高三11月學段考試數學理科試題 題型:013
用a、b、c表示不同的直線,r表示平面,給出下列命題:
(1)若a∥b,b∥c,則a∥c
(2)若a⊥b,b⊥c,則a⊥c
(3)若a∥r,b∥r,則a∥b
(4)若a⊥r,b⊥r,則a∥b
其中真命題的序號是
(1)(2)
(2)(3)
(1)(4)
(3)(4)
查看答案和解析>>
科目:高中數學 來源:江蘇省栟茶高級中學2012屆高三第一次學情調研測試數學試題 題型:022
設a,b為不重合的兩條直線,α,β為不重合的兩個平面,給出下列命題:
(1)若a∥α且b∥α,則a∥b;
(2)若a⊥α且a⊥β,則α∥β;
(3)若![]()
![]() ,則一定存在平面γ,使得
,則一定存在平面γ,使得![]() ;
;
(4)若![]()
![]() ,則一定存在直線l,使得
,則一定存在直線l,使得![]() .
.
上面命題中,所有真命題的序號是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com