在△ABC中,“A>B”是“sinA>sinB”成立的( )
A.充要條件
B.2充分部必要條件
C.必要不充分條件
D.既不充分也不必要條件
【答案】
分析:考查四個選項知,可先證充分性,由,“A>B”推導“sinA>sinB”,分A是銳角與A不是銳角兩類證明即可;再證必要性,由于在(0,π)上正弦函數不是單調函數,可分兩類證明,當A是鈍角時,與A不是鈍角時,易證,再由充分條件必要條件的定義得出正確選項即可
解答:解:1°由題意,在△ABC中,“A>B”,由于A+B<π,必有B<π-A
若A,B都是銳角,顯然有“sinA>sinB”成立,
若A,B之一為銳角,必是B為銳角,此時有π-A不是鈍角,由于A+B<π,必有B<π-A≤
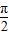
,此時有sin(π-A)=sinA>sinB
綜上,△ABC中,“A>B”是“sinA>sinB”成立的充分條件
2°研究sinA>sinB,若A不是銳角,顯然可得出A>B,若A是銳角,亦可得出A>B,
綜上在△ABC中,“A>B”是“sinA>sinB”成立的必要條件
綜合1°,2°知,在△ABC中,“A>B”是“sinA>sinB”成立的充要條件,
故選A
點評:本題考查充要條件的判斷,證明充要條件要分兩步證明,先證充分性再證必要性,解題的關鍵是理解題意及充要條件證明的方法,本題考查到了分類討論的思想,考查了推理判斷的能力.

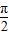 ,此時有sin(π-A)=sinA>sinB
,此時有sin(π-A)=sinA>sinB

 高中必刷題系列答案
高中必刷題系列答案