
【題目】已知橢圓![]() 的中心在原點,焦點在
的中心在原點,焦點在![]() 軸上,橢圓的一個頂點為
軸上,橢圓的一個頂點為![]() ,右焦點
,右焦點![]() 到直線
到直線![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若過![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() ,且
,且![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,
兩點,![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,求四邊形
兩點,求四邊形![]() 的面積的取值范圍.
的面積的取值范圍.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】“十三五”規劃確定了到2020年消除貧困的宏偉目標,打響了精準扶貧的攻堅戰,為完成脫貧任務,某單位在甲地成立了一家醫療器械公司吸納附近貧困村民就工,已知該公司生產某種型號醫療器械的月固定成本為20萬元,每生產1千件需另投入5.4萬元,設該公司一月內生產該型號醫療器械x千件且能全部銷售完,每千件的銷售收入為![]() 萬元,已知
萬元,已知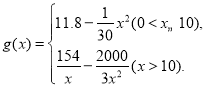
(1)請寫出月利潤y(萬元)關于月產量x(千件)的函數解析式;
(2)月產量為多少千件時,該公司在這一型號醫療器械的生產中所獲月利潤最大?并求出最大月利潤(精確到0.1萬元).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個函數![]() ,如果對任意一個三角形,只要它的三邊長
,如果對任意一個三角形,只要它的三邊長![]() 、
、![]() 、
、![]() 都在
都在![]() 的定義域內,就有
的定義域內,就有![]() 、
、![]() 、
、![]() 也是某個三角形的三邊長,則稱
也是某個三角形的三邊長,則稱![]() 為“保三角形函數”.
為“保三角形函數”.
(1)若![]() 是定義在
是定義在![]() 上的周期函數,且值域為
上的周期函數,且值域為![]() ,證明:
,證明:![]() 不是保三角形函數;
不是保三角形函數;
(2)若![]() 是保三角形函數,求
是保三角形函數,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司新上一條生產線,為保證新的生產線正常工作,需對該生產線進行檢測,現從該生產線上隨機抽取100件產品,測量產品數據,用統計方法得到樣本的平均數![]() ,標準差
,標準差![]() ,繪制如圖所示的頻率分布直方圖,以頻率值作為概率估值.
,繪制如圖所示的頻率分布直方圖,以頻率值作為概率估值.
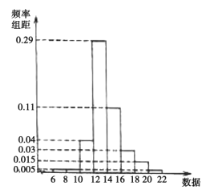
(1)從該生產線加工的產品中任意抽取一件,記其數據為X,依據以下不等式評判(P表示對應事件的概率)
①![]()
②![]()
③![]()
評判規則為:若至少滿足以上兩個不等式,則生產狀況為優,無需檢修;否則需檢修生產線,試判斷該生產線是否需要檢修;
(2)將數據不在![]() 內的產品視為次品,從該生產線加工的產品中任意抽取2件,次品數記為Y,求Y的分布列與數學期望
內的產品視為次品,從該生產線加工的產品中任意抽取2件,次品數記為Y,求Y的分布列與數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
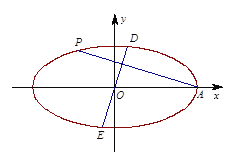
【題目】已知橢圓![]()
![]() 的右頂點
的右頂點![]() ,離心率為
,離心率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知![]() (異于點
(異于點![]() )為橢圓
)為橢圓![]() 上一個動點,過
上一個動點,過![]() 作線段
作線段![]() 的垂線
的垂線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一個三角形的邊長與面積都是整數,則稱為“海倫三角形”;三邊長互質的海倫三角形,稱為“本原海倫三角形”;邊長都不是3的倍數的本原海倫三角形,稱為“奇異三角形”.
(1)求奇異三角形的最小邊長的最小值;
(2)求證:等腰的奇異三角形有無數個;
(3)問:非等腰的奇異三角形有多少個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com