
| |||||||||||||||
(1) |
解析:橢圓C的焦點在x軸上,由橢圓上的點A到F1、F2兩點的距離之和是4,得2a=4,即a=2. 又點A(1, 所以橢圓C的方程為 |
(2) |
設橢圓C上的動點為K(x1,y1),線段F1K的中點Q(x,y)滿足x= 因此 |
(3) |
類似的性質為:若M、N是雙曲線 設點M的坐標為(m,n),則點N的坐標為(-m,-n),其中 又設點P的坐標為(x,y),由kPM= 點評:本題主要考查橢圓的基本知識及求動點軌跡方程的常用方法.第(3)問對考生的聯想、類比、邏輯思維及運算能力都有較高的要求,根據提供的信息,讓考生通過類比自己找到所證問題,這是高考數學命題的方向.應引起注意. |


 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 (a>b>0)的左、右兩個焦點,橢圓C上的點
(a>b>0)的左、右兩個焦點,橢圓C上的點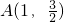 到兩點的距離之和等于4.
到兩點的距離之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com