數學英語物理化學 生物地理
數學英語已回答習題未回答習題題目匯總試卷匯總
思路分析：△F1PF2的面積是由兩個焦點和雙曲線上的一個點構成，找出∠F1PF2=60°的兩邊考慮用余弦定理求得.
解:|F1F2|2=4c2=4×(24+16)=160.
在△F1PF2中,由余弦定理,得|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos60°.
∴|PF1|2+|PF2|2-|PF1||PF2|=160 ①
又∵|PF1|-|PF2|=±,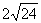
∴|PF1|2-2|PF1||PF2|+|PF2|2=96 ②
①-②,得|PF1|·|PF2|=64.
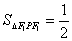∴|PF1|·|PF2|·sin60°=×64×.
科目：高中數學 來源： 題型：
已知雙曲線-=1,P為雙曲線上一點，F1、F2是雙曲線的兩個焦點，并且∠F1PF2=60°，求△F1PF2的面積.
百度致信 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
=1,P為雙曲線上一點,F1、F2是雙曲線的兩個焦點,并且∠F1PF2=60°,求△F1PF2的面積.
|PF1|·|PF2|·sin60°=
×64×
.
-
=1,P為雙曲線上一點 ，F1、 F2是雙曲線的兩個焦點 ，并且∠F1PF2=60°，求△F1PF2的面積.
-
=1,P為雙曲線上一點，F1、F2是雙曲線的兩個焦點，并且∠F1PF2=60°，求△F1PF2的面積.
=1,P為雙曲線上一點.F1、F2是雙曲線的兩個焦點，并且∠F1PF2=60°,求△F1PF2的面積.
=1,P為雙曲線上一點.F1、F2是雙曲線的兩個焦點，并且∠F1PF2=60°,求△F1PF2的面積.