
【題目】已知函數![]()
![]() 的部分圖象如圖所示.
的部分圖象如圖所示.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函數![]() 在
在![]() 上的單調區間;
上的單調區間;
(Ⅲ)若對任意![]() 都有
都有![]() ,求實數m的取值范圍.
,求實數m的取值范圍.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)單調遞增區間為
;(Ⅱ)單調遞增區間為![]() 和
和![]() ,單調遞減區間為
,單調遞減區間為![]() ;(Ⅲ)
;(Ⅲ)![]() ;
;
【解析】
(Ⅰ)根據三角函數的部分圖象求出![]()
![]() 和
和![]() 的值;
的值;
(Ⅱ)由(Ⅰ)寫出函數![]() 的解析式,再求函數在
的解析式,再求函數在![]() ,
,![]() 上的單調遞增區間和單調遞減區間;
上的單調遞增區間和單調遞減區間;
(Ⅲ)由(Ⅱ)求出函數![]() 在
在![]() ,
,![]() 的最大值和最小值,得出
的最大值和最小值,得出![]() 的最大值,從而求得
的最大值,從而求得![]() 的取值范圍.
的取值范圍.
(Ⅰ)設函數![]() 的最小正周期為
的最小正周期為![]() ,
,
由圖可知,![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ;
;
又![]() ,所以
,所以![]() ,
,
因為![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ;
;
(Ⅱ)由(Ⅰ)知,![]() ,
,
因為當![]() 時,
時,![]() ,
,
所以當![]() ,即
,即![]() 時,
時,![]() 單調遞增;
單調遞增;
當![]() ,即
,即![]() 時,
時,![]() 單調遞減;
單調遞減;
當![]() ,即
,即![]() 時,
時,![]() 單調遞增.
單調遞增.
所以函數![]() 單調遞增區間為
單調遞增區間為![]() 和
和![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
(Ⅲ)由(Ⅱ)可知,函數![]() 在
在![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]() ,
,
所以對任意![]() ,都有
,都有![]() ,
,
且當![]() ,
,![]() 時,
時,![]() 取到最大值
取到最大值![]() ,
,
又因為對任意![]() ,都有
,都有![]() 成立,
成立,
所以![]() ,即
,即![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】節約資源和保護環境是中國的基本國策.某化工企業,積極響應國家要求,探索改良工藝,使排放的廢氣中含有的污染物數量逐漸減少.已知改良工藝前所排放的廢氣中含有的污染物數量為![]() ,首次改良后所排放的廢氣中含有的污染物數量為
,首次改良后所排放的廢氣中含有的污染物數量為![]() .設改良工藝前所排放的廢氣中含有的污染物數量為
.設改良工藝前所排放的廢氣中含有的污染物數量為![]() ,首次改良工藝后所排放的廢氣中含有的污染物數量為
,首次改良工藝后所排放的廢氣中含有的污染物數量為![]() ,則第n次改良后所排放的廢氣中的污染物數量
,則第n次改良后所排放的廢氣中的污染物數量![]() ,可由函數模型
,可由函數模型![]() 給出,其中n是指改良工藝的次數.
給出,其中n是指改良工藝的次數.
(1)試求改良后所排放的廢氣中含有的污染物數量的函數模型;
(2)依據國家環保要求,企業所排放的廢氣中含有的污染物數量不能超過![]() ,試問至少進行多少次改良工藝后才能使得該企業所排放的廢氣中含有的污染物數量達標.
,試問至少進行多少次改良工藝后才能使得該企業所排放的廢氣中含有的污染物數量達標.
(參考數據:取![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】襄陽市擬在2021年奧體中心落成后申辦2026年湖北省省運會,據了解,目前武漢,宜昌,黃石等申辦城市因市民擔心賽事費用超支而準備相繼退出,某機構為調查襄陽市市民對申辦省運會的態度,選取某小區的100位居民調查結果統計如下:
支持 | 不支持 | 合計 | |
年齡不大于50歲 | 60 | ||
年齡大于50歲 | 10 | ||
合計 | 80 | 100 |
(1)根據已知數據,把表格數據填寫完整;
(2)能否在犯錯誤的概率不超過![]() 的前提下認為不同年齡與支持申辦省運會無關?
的前提下認為不同年齡與支持申辦省運會無關?
附: ![]() ,
, ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人做試驗,從一個裝有標號為1,2,3,4的小球的盒子中,無放回地取兩個小球,每次取一個,先取的小球的標號為![]() ,后取的小球的標號為
,后取的小球的標號為![]() ,這樣構成有序實數對
,這樣構成有序實數對![]()
(1)寫出這個試驗的所有結果;
(2)求“第一次取出的小球上的標號為![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從高三抽出![]() 名學生參加數學競賽,由成績得到如下的頻率分布直方圖.試利用頻率分布直方圖求:
名學生參加數學競賽,由成績得到如下的頻率分布直方圖.試利用頻率分布直方圖求:
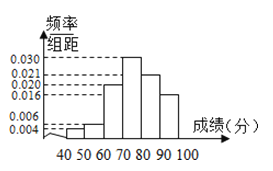
(1)這![]() 名學生成績的眾數與中位數;
名學生成績的眾數與中位數;
(2)這![]() 名學生的平均成績.
名學生的平均成績.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,函數
,函數![]() .
.
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)若關于![]() 的方程
的方程![]() 的解集中恰有一個元素,求
的解集中恰有一個元素,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若對任意
,若對任意![]() ,函數
,函數![]() 在區間
在區間![]() 上的最大值與最小值的差不超過1,求
上的最大值與最小值的差不超過1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從分別寫有1,2,3,4的4張卡片中隨機抽取1張,放回后再隨機抽取1張,則抽得的第一張卡片上的數大于第二張卡片上的數的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著我國互聯網信息技術的發展,網絡購物已經成為許多人消費的一種重要方式,某市為了了解本市市民的網絡購物情況,特委托一家網絡公示進行了網絡問卷調查,并從參與調查的10000名網民中隨機抽取了200人進行抽樣分析,得到了下表所示數據:
經常進行網絡購物 | 偶爾或從不進行網絡購物 | 合計 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合計 | 110 | 90 | 200 |
(1)依據上述數據,能否在犯錯誤的概率不超過![]() 的前提下認為該市市民進行網絡購物的情況與性別有關?
的前提下認為該市市民進行網絡購物的情況與性別有關?
(2)現從所抽取的女性網民中利用分層抽樣的方法再抽取![]() 人,從這
人,從這![]() 人中隨機選出
人中隨機選出![]() 人贈送網絡優惠券,求出選出的
人贈送網絡優惠券,求出選出的![]() 人中至少有兩人是經常進行網絡購物的概率;
人中至少有兩人是經常進行網絡購物的概率;
(3)將頻率視為概率,從該市所有的參與調查的網民中隨機抽取![]() 人贈送禮物,記經常進行網絡購物的人數為
人贈送禮物,記經常進行網絡購物的人數為![]() ,求
,求![]() 的期望和方差.
的期望和方差.
附:![]() ,其中
,其中![]()

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為自然對數的底數,
為自然對數的底數,![]() .
.
(1)討論函數![]() 的單調性,并寫出相應的單調區間;
的單調性,并寫出相應的單調區間;
(2)已知![]() ,
,![]() ,若
,若![]() 對任意
對任意![]() 都成立,求
都成立,求![]() 的最大值;
的最大值;
(3)設![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com