
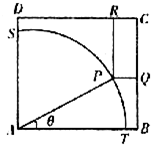
 隨著機動車數量的增加,對停車場所的需求越來越大,如圖,ABCD是一塊邊長為100米的正方形地皮,其中ATPS是一座半徑為90米的扇形小山,P是弧TS上一點,其余部分都是平地,現一開發商想在平地上建一個邊落在BC和CD上的長方形停車場PQCR.
隨著機動車數量的增加,對停車場所的需求越來越大,如圖,ABCD是一塊邊長為100米的正方形地皮,其中ATPS是一座半徑為90米的扇形小山,P是弧TS上一點,其余部分都是平地,現一開發商想在平地上建一個邊落在BC和CD上的長方形停車場PQCR.
 ),可得t2=(sinθ+cosθ)2=1+2sinθcosθ,
),可得t2=(sinθ+cosθ)2=1+2sinθcosθ,
 =
= ×
× +950
+950 時,Smax=14050-9000
時,Smax=14050-9000 (m2),t=
(m2),t= 時,Smin=950(m2).
時,Smin=950(m2).

科目:高中數學 來源: 題型:
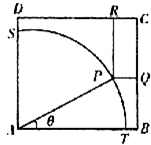 隨著機動車數量的增加,對停車場所的需求越來越大,如圖,ABCD是一塊邊長為100米的正方形地皮,其中ATPS是一座半徑為90米的扇形小山,P是弧TS上一點,其余部分都是平地,現一開發商想在平地上建一個邊落在BC和CD上的長方形停車場PQCR.
隨著機動車數量的增加,對停車場所的需求越來越大,如圖,ABCD是一塊邊長為100米的正方形地皮,其中ATPS是一座半徑為90米的扇形小山,P是弧TS上一點,其余部分都是平地,現一開發商想在平地上建一個邊落在BC和CD上的長方形停車場PQCR.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com