
若f(x)的定義域為[a,b],值域為[a,b](a<b),則稱函數f(x)是[a,b]上的“四維光軍”函數.
①設g(x)= x2-x+
x2-x+ 是[1,b]上的“四維光軍”函數,求常數b的值;
是[1,b]上的“四維光軍”函數,求常數b的值;
②問是否存在常數a,b(a>-2),使函數h(x)= 是區間[a,b]上的“四維光軍”函數?若存在,求出a,b的值,否則,請說明理由.
是區間[a,b]上的“四維光軍”函數?若存在,求出a,b的值,否則,請說明理由.
①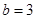 ; ②不存在,詳見解析
; ②不存在,詳見解析
【解析】
試題分析:①根據信息找到b所滿足的等式即可求出b的值,一定要先判斷函數在閉區間上的單調性;②先假設存在題目要求的常數,根據“四維光軍”函數的特性去找到此常數能得到的結論,推出矛盾即可說明這樣的常數是不存在的,這是一種逆向思維的題目,首先假設存在,由存在得出矛盾,則可知存在不成立.
試題解析:①由已知得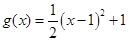 ,其對稱軸為
,其對稱軸為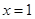 ,區間
,區間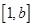 在對稱軸的右邊,
在對稱軸的右邊,
所以函數在區間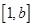 上是單調遞增的,
3分
上是單調遞增的,
3分
由“四維光軍”函數的定義可知,
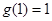 ,
,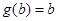 即
即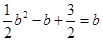 ,又因為
,又因為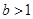 ,解得
,解得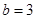 ;
6分
;
6分
②假如函數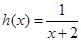 在區間
在區間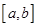
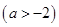 上是“四維光軍”函數,
7分
上是“四維光軍”函數,
7分
因為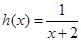 在區間
在區間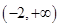 是單調遞減函數,則有
是單調遞減函數,則有 ,
10分
,
10分
即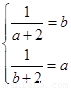 ,解得
,解得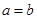 ,這與已知矛盾.
12分
,這與已知矛盾.
12分
考點:函數單調性的應用,函數的圖形和性質的應用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 目標測試系列答案
目標測試系列答案科目:高中數學 來源: 題型:
已知函數f(x)=lg[(a2-1)x2+(a+1)x+1]
(1)若f(x)的定義域為(-∞,+∞),求實數a的取值范圍;
(2)若f(x)的值域為(-∞,+∞),求實數a的取值范圍![]()
查看答案和解析>>
科目:高中數學 來源:2012年人教B版高中數學必修一3.2對數函數練習卷(二)(解析版) 題型:解答題
.已知函數f(x)=lg[(a2-1)x2+(a+1)x+1],若f(x)的定義域為R,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年浙江省高三上學期第一次月考數學理卷 題型:解答題
(本小題滿分14分)
已知0是坐標原點, ,
,
(I) 的單調遞增區間;
的單調遞增區間;
(II)若f(x)的定義域為 ,值域為[2,5],求m的值。
,值域為[2,5],求m的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com