
(本題滿分16分)設函數y=f(x)對任意實數x,都有f(x)=2f(x+1),當x∈[0,1]時,f(x)=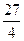 x2(1-x).
x2(1-x).
(Ⅰ)已知n∈N+,當x∈[n,n+1]時,求y=f(x)的解析式;
(Ⅱ)求證:對于任意的n∈N+,當x∈[n,n+1]時,都有|f(x)|≤ ;
;
(Ⅲ)對于函數y=f(x) (x∈[0,+∞
(x∈[0,+∞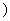 ,若在它的圖象上存在點P,使經過點P的切線與直線x+y=1平行,那么這樣點有多少個?并說明理由
,若在它的圖象上存在點P,使經過點P的切線與直線x+y=1平行,那么這樣點有多少個?并說明理由
解:(Ⅰ)由f(x)=2f(x+1)→f(x)= (x-1),x∈[n,n+1],則(x-n)∈[0,1]
(x-1),x∈[n,n+1],則(x-n)∈[0,1]
→f(x-n)=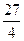 (x-n)2(1+n-x). f(x)=
(x-n)2(1+n-x). f(x)= f(x-1)=
f(x-1)=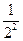 f(x-2)=…=
f(x-2)=…= f(x-n)=
f(x-n)=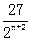 (x-n)2(1+n-x). (n=0也適用). ………………4分
(x-n)2(1+n-x). (n=0也適用). ………………4分
(Ⅱ)f
 (x)=
(x)=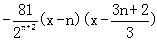 ,由f
,由f (x)=0得x=n或x=n+
(x)=0得x=n或x=n+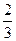
f(x)的極大值為f(x)的最大值, x n (n,n+ 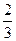 )
)n+ 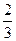
(n+ 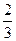 ,n+1)
,n+1)n+1 f  (x)
(x) + 0 - + 0 ↗[來源:學&科&網] 極大 ↘ 0 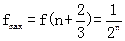 ,
,
又f(x)≥f(n)=f(n+1)=0,∴|f(x)|=f(x)≤ (x∈[n,n+1]).…8分
(x∈[n,n+1]).…8分
(Ⅲ)y=f(x),x∈[0,+∞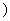 即為y=f(x),x∈[n,n+1],f
即為y=f(x),x∈[n,n+1],f (x)="-1."
(x)="-1."
本題轉化為方程f
 (x)=-1在[n,n+1]上有解問題
(x)=-1在[n,n+1]上有解問題
即方程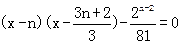 在[n,n+1]內是否有解. ……11分
在[n,n+1]內是否有解. ……11分
令g(x)=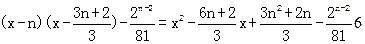 ,
,
對軸稱x=n +
+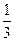 ∈[n,n+1],
∈[n,n+1],
又△=…=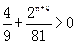 ,g(n)=
,g(n)=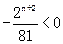 ,g(n+1)=
,g(n+1)=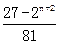 ,
,
①當0≤n≤2時,g(n+1)≥0,∴方程g(x)=0在區間[0,1],[1,2],[2,3]上分別有一解,即存在三個點P;
②n≥3時,g(n+1)<0,方程g(x)=0在[n,n+1]上無解,即不存在這樣點P.
綜上所述:滿足條件的點P有三個. …………………………16分
解析


科目:高中數學 來源:2010年江蘇省海門中學高一下學期期末考試數學卷 題型:解答題
(本題滿分16分)
設正項等差數列 的前n項和為
的前n項和為 ,其中
,其中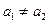 .
. 是數列
是數列 中滿足
中滿足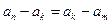 的任意項.
的任意項.
(1)求證: ;
;
(2)若 也成等差數列,且
也成等差數列,且 ,求數列
,求數列 的通項公式;
的通項公式;
(3)求證: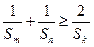 .
.
查看答案和解析>>
科目:高中數學 來源:2010年江蘇省鹽城中學高一下學期期末考試數學卷 題型:解答題
(本題滿分16分)
設 是圓心在拋物線
是圓心在拋物線 上的一系列圓,它們的圓心的橫坐標分別記為
上的一系列圓,它們的圓心的橫坐標分別記為 ,已知
,已知 ,又
,又
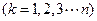 都與
都與 軸相切,且順次逐個相鄰外切. WWW.K**S*858$$U.COM
軸相切,且順次逐個相鄰外切. WWW.K**S*858$$U.COM
(1)求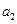 ;
;
(2)求由 構成的數列
構成的數列 的通項公式;
的通項公式;
(3)求證: .
.
查看答案和解析>>
科目:高中數學 來源:2010年江蘇省范集中學高一下學期期末考試數學卷 題型:解答題
(本題滿分16分)
設數列 滿足
滿足 ,令
,令 .
.
⑴試判斷數列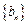 是否為等差數列?并說明理由;
是否為等差數列?并說明理由;
⑵若 ,求
,求 前
前 項的和
項的和 ;
;
⑶是否存在 使得
使得 三數成等比數列?
三數成等比數列?
查看答案和解析>>
科目:高中數學 來源:2013屆江蘇省南通市高二期中聯考數學試卷 題型:解答題
(本題滿分16分)設橢圓 的左,右兩個焦點分別為
的左,右兩個焦點分別為 ,短軸的上端點為
,短軸的上端點為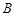 ,短軸上的兩個三等分點為
,短軸上的兩個三等分點為 ,且
,且 為正方形。
為正方形。
(1)求橢圓的離心率;
(2)若過點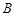 作此正方形的外接圓的切線在
作此正方形的外接圓的切線在 軸上的一個截距為
軸上的一個截距為 ,求此橢圓方程。
,求此橢圓方程。

查看答案和解析>>
科目:高中數學 來源:江蘇省淮安市淮陰區2009-2010學年度第二學期期末高一年級調查測試數學試題 題型:解答題
(本題滿分16分)
設數列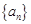 的前
的前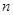 項和為
項和為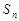 ,若對任意
,若對任意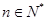 ,都有
,都有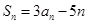 .
.
⑴求數列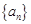 的首項;
的首項;
⑵求證:數列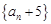 是等比數列,并求數列
是等比數列,并求數列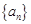 的通項公式;
的通項公式;
⑶數列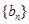 滿足
滿足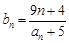 ,問是否存在
,問是否存在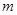 ,使得
,使得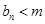 恒成立?如果存在,求出
恒成立?如果存在,求出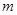 的值,如果不存在,說明理由.
的值,如果不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com