
分析 P(ξ)是“ξ個人命中,3-ξ個人未命中”的概率.其中ξ的可能取值為0,1,2,3.則P(ξ=1)-P(ξ=0)≥0,P(ξ=1)-P(ξ=2)≥0,P(ξ=1)-P(ξ=3)≥0.及其0<a<1,解出即可得出.
解答 解:P(ξ)是“ξ個人命中,3-ξ個人未命中”的概率.其中ξ的可能取值為0,1,2,3.
P(ξ=0)=${C}_{1}^{0}•(1-\frac{1}{2})$•${∁}_{2}^{0}(1-a)^{2}$=$\frac{1}{2}(1-a)^{2}$,P(ξ=1)=${∁}_{1}^{1}•\frac{1}{2}{∁}_{2}^{0}(1-a)^{2}$+${∁}_{1}^{0}(1-\frac{1}{2})•{∁}_{2}^{1}a(1-a)$=$\frac{1}{2}(1-{a}^{2})$,
P(ξ=2)=${∁}_{1}^{1}•\frac{1}{2}•{∁}_{2}^{1}a(1-a)$+${∁}_{1}^{0}(1-\frac{1}{2}){∁}_{2}^{2}{a}^{2}$=$\frac{1}{2}(2a-{a}^{2})$,P(ξ=3)=${∁}_{1}^{1}•\frac{1}{2}•{∁}_{2}^{2}$a2=$\frac{1}{2}{a}^{2}$.
P(ξ=1)-P(ξ=0)=$\frac{1}{2}(1-{a}^{2})$-$\frac{1}{2}(1-a)^{2}$=a(1-a),
P(ξ=1)-P(ξ=2)=$\frac{1}{2}(1-{a}^{2})$-$\frac{1}{2}(2a-{a}^{2})$=$\frac{1-2a}{2}$,
P(ξ=1)-P(ξ=3)=$\frac{1}{2}(1-{a}^{2})$-$\frac{1}{2}{a}^{2}$=$\frac{1-2{a}^{2}}{2}$.
由a(1-a)≥0,$\frac{1-2a}{2}$≥0,$\frac{1-2{a}^{2}}{2}$≥0,0<a<1,得$0<a≤\frac{1}{2}$,即a的取值范圍是$(0,\frac{1}{2}]$.
故答案為:$(0,\frac{1}{2}]$.
點評 本題考查了相互獨立事件與互斥事件的概率計算公式及其性質、不等式的解法,考查了推理能力與計算能力,屬于中檔題.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
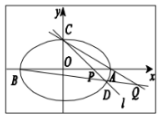 過點C(0,$\sqrt{2}$)的橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,橢圓與x軸交于兩點A(a,0),B(-a,0),過點C的直線l與橢圓交于另一點D,并與x軸交于點P,直線AC與BD交于點Q.
過點C(0,$\sqrt{2}$)的橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,橢圓與x軸交于兩點A(a,0),B(-a,0),過點C的直線l與橢圓交于另一點D,并與x軸交于點P,直線AC與BD交于點Q.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
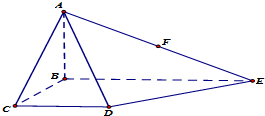 如圖,在四棱錐A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,點F為AE的中點.
如圖,在四棱錐A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,點F為AE的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ¬p:?x0∈A,2x0∈B | B. | ¬p:?x0∉A,2x0∈B | C. | ¬p:?x0∈A,2x0∉B | D. | ¬p:?x∉A,2x∉B |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com