Question

已知曲線C滿足方程=|1+ax|(a＞0為常數).

(1)判斷曲線的形狀;

(2)若直線l：y=x+a交曲線C于點P、Q，線段PQ中點的橫坐標為-，試問在曲線C上是否存在不同的兩點A，B關于直線l對稱?

 

Answer 1

解：(1)∵=|1+ax|,

∴(x+a)²+y²=(1+ax)².

∴(1-a²)x²+y²=1-a².

∴當0＜a＜1時，表示焦點在x軸上的橢圓；

當a=1時，表示x軸所在的直線；

當a＞1時，表示焦點在x軸上的雙曲線.

(2)設P(x₁，y₁)，Q(x₂，y₂)，聯立方程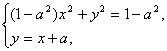：得(2-a²)x²+2ax+2a²-1=0.

設(2-a²)x²+2ax+2a²-1=0的兩根為x₁，x₂，

∴                                                   

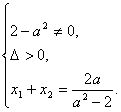
由題意=-，a＞0，取a=3，則曲線C：x²-=1..l:y=x+3

假設曲線C上存在A（x_3，y₃）B(x₄,y₄)關于l對稱，設AB的中點M（x₀,y₀）,由點差法，可得AB的斜率k_AB=,又y₀=x₀+3, ∴M().∴AB:y+, 代入曲線C：x^2-有△＞0，∴曲線C上存在不同的兩點A、B關于直線l對稱。