(14分)
設集合W由滿足下列兩個條件的數列
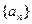
構成:
①
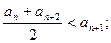
②存在實數M,使
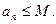
(n為正整數)
(I)在只有5項的有限數列
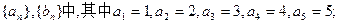
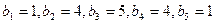
;試判斷數列
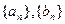
是否為集合W的元素;
(II)設
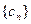
是等差數列,
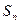
是其前n項和,
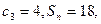
證明數列
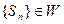
;并寫出M的取值范圍;
(III)設數列
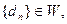
且對滿足條件的常數M,存在正整數k,使
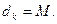
求證:
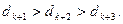
(I)對于數列
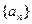
,當n=1時,
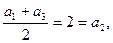
顯然不滿足集合W的條件,①
故
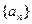
不是集合W中的元素, …………2分
對于數列
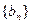
,當
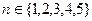
時,
不僅有
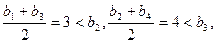
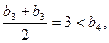
而且有
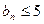
,
顯然滿足集合W的條件①②,
故
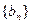
是集合W中的元素. …………4分
(II)
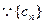
是等差數列,
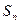
是其前n項和,
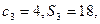
設其公差為d,
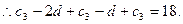
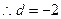
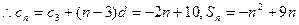
…………7分

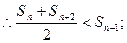
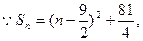

的最大值是
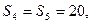
即
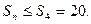
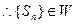
,且M的取值范圍是
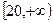
…………9分
(III)證明:
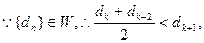
整理

,
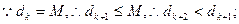
又

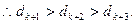
…………14分
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
(本小題滿分13分)
設
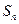
是數列
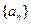
(
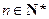
)的前
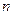
項和,
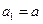
,且
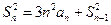
,
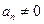
,
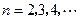
.
(I)證明:數列
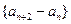
(
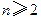
)是常數數列;
(II)試找出一個奇數
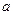
,使以18為首項,7為公比的等比數列
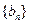
(
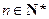
)中的所有項都是數列
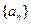
中的項,并指出
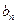
是數列
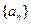
中的第幾項.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(本小題滿分12 分)
已知{
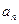
}是整數組成的數列,a
1 = 1,且點
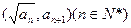
在函數
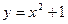
的圖象上,
(1)求數列{
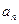
}的通項公式;
(2)若數列{
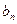
}滿足
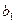
= 1,
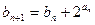
,求證:
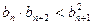
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
若數列{
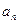
}的前n項和為
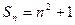
,則 ( )
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
(滿分10分)已知數列
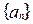
,
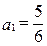
,若以
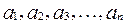
為系數的二次方程
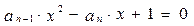
都有根
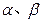
,且滿足
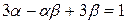
。
(1)求數列
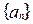
通項公式;
(2)求數列
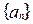
前
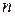
項和
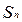
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
一個數字生成器,生成規則如下:第1次生成一個數
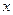
,以后每次生成的結果可將上一次生成的每一個數
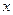
生成兩個數,一個是
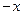
,另一個是
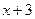
.設第
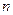
次生成的數的個數為
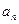
,則數列
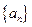
的前
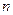
項和
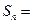
_________________;若

,前
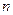
次生成的所有數中不同的數的個數為
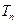
,則
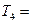
______________________.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
已知
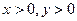
,且
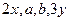
成等差數列,
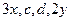
成等比數列,則
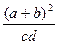
的最小值為 ( )
A.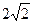 | B.2 | C.4 | D.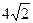 |
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
已知數列{ a
n }滿足條件a
1 =" –2" , a
n + 1 ="2" +
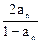
, 則a
5 =
查看答案和解析>>
主站蜘蛛池模板:
欧美一级日韩
|
亚洲人网站
|
久久久久久久久国产成人免费
|
欧美日韩精品一区二区三区蜜桃
|
亚洲精品久久久久久久久久久久久
|
亚洲不卡网站
|
日韩精品无吗
|
在线中文字幕日韩
|
欧美在线免费视频
|
国产99页|
日韩精品在线观看一区
|
中文二区|
日韩美女爱爱
|
久久综合久久受
|
久久精品毛片
|
一区二区三区四区免费观看
|
精品国产乱码久久久久久影片
|
青青草视频在线免费观看
|
精品国产高清一区二区三区
|
日韩激情网站
|
日韩成人在线视频
|
亚洲成人av
|
亚洲欧美日韩另类精品一区二区三区
|
日本在线高清
|
亚洲免费视频在线观看
|
日韩av视屏|
日韩免费在线
|
91麻豆精品国产91久久久久久
|
黄页视频在线免费观看
|
欧美精品99
|
成人教育av|
精品国产乱码久久
|
久久免费精品
|
久久国产欧美日韩精品
|
国产精品久久久久无码av
|
aaa在线
|
日韩在线成人
|
91大神在线看
|
免费激情网站
|
中文字幕国产在线观看
|
www久久精品
|

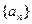 構成:
構成: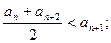
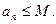 (n為正整數)
(n為正整數)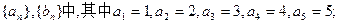
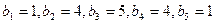 ;試判斷數列
;試判斷數列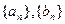 是否為集合W的元素;
是否為集合W的元素;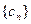 是等差數列,
是等差數列,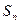 是其前n項和,
是其前n項和,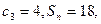 證明數列
證明數列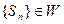 ;并寫出M的取值范圍;
;并寫出M的取值范圍;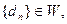 且對滿足條件的常數M,存在正整數k,使
且對滿足條件的常數M,存在正整數k,使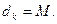
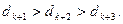
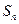 是數列
是數列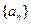 (
(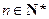 )的前
)的前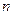 項和,
項和,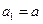 ,且
,且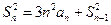 ,
,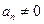 ,
,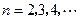 .
.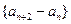 (
(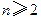 )是常數數列;
)是常數數列;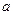 ,使以18為首項,7為公比的等比數列
,使以18為首項,7為公比的等比數列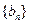 (
(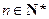 )中的所有項都是數列
)中的所有項都是數列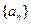 中的項,并指出
中的項,并指出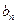 是數列
是數列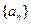 中的第幾項.
中的第幾項.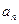 }是整數組成的數列,a1 = 1,且點
}是整數組成的數列,a1 = 1,且點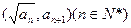 在函數
在函數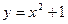 的圖象上,
的圖象上,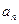 }的通項公式;
}的通項公式;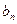 }滿足
}滿足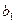 = 1,
= 1,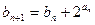 ,求證:
,求證: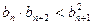
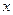 ,以后每次生成的結果可將上一次生成的每一個數
,以后每次生成的結果可將上一次生成的每一個數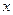 生成兩個數,一個是
生成兩個數,一個是 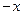 ,另一個是
,另一個是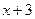 .設第
.設第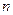 次生成的數的個數為
次生成的數的個數為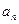 ,則數列
,則數列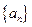 的前
的前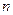 項和
項和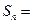 _________________;若
_________________;若 ,前
,前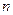 次生成的所有數中不同的數的個數為
次生成的所有數中不同的數的個數為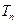 ,則
,則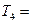 ______________________.
______________________.