
【題目】設(shè)函數(shù)![]()
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 有兩個(gè)零點(diǎn)
有兩個(gè)零點(diǎn)![]() ,
,![]() ,求滿足條件的最小正整數(shù)a的值.
,求滿足條件的最小正整數(shù)a的值.
【答案】(1)當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 單調(diào)遞增區(qū)間為
單調(diào)遞增區(qū)間為![]() ,無(wú)單調(diào)減區(qū)間
,無(wú)單調(diào)減區(qū)間
當(dāng)![]() 時(shí), 函數(shù)的單調(diào)增區(qū)間為
時(shí), 函數(shù)的單調(diào)增區(qū)間為![]() ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為![]()
(2) 滿足條件的最小正整數(shù)a的值為3
【解析】
(1)求導(dǎo)得![]() ,故分
,故分![]() 與
與![]() 兩種情況進(jìn)行討論即可.
兩種情況進(jìn)行討論即可.
(2)由(1)知![]() ,
,![]() 的最小值
的最小值![]() ,再整理化簡(jiǎn)令
,再整理化簡(jiǎn)令![]() ,再分析零點(diǎn)所在區(qū)間進(jìn)行討論即可.
,再分析零點(diǎn)所在區(qū)間進(jìn)行討論即可.
(1)![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上恒成立,
上恒成立,
所以函數(shù)![]() 單調(diào)遞增區(qū)間為
單調(diào)遞增區(qū)間為![]() ,此時(shí)
,此時(shí)![]() 無(wú)單調(diào)減區(qū)間.
無(wú)單調(diào)減區(qū)間.
當(dāng)![]() 時(shí),由
時(shí),由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,得
,得![]() ,
,
所以函數(shù)的單調(diào)增區(qū)間為![]() ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為![]()
(2)由(1)可知函數(shù)![]() 有兩個(gè)零點(diǎn),
有兩個(gè)零點(diǎn),
所以![]() ,
,![]() 的最小值
的最小值![]() ,即
,即![]() .
.
因?yàn)?/span>![]() ,所以
,所以![]() .
.
令![]() ,顯然
,顯然![]() 在
在![]() 上為增函數(shù),且
上為增函數(shù),且![]() ,
,![]() ,
,
所以存在![]() ,
,![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() ,
,
所以滿足條件的最小正整數(shù)![]() .
.
又當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,
,
所以![]() 時(shí),
時(shí),![]() 有兩個(gè)零點(diǎn).
有兩個(gè)零點(diǎn).
綜上所述,滿足條件的最小正整數(shù)a的值為3.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(Ⅰ)若![]() 在
在![]() 內(nèi)單調(diào)遞減,求實(shí)數(shù)
內(nèi)單調(diào)遞減,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)若函數(shù)![]() 有兩個(gè)極值點(diǎn)分別為
有兩個(gè)極值點(diǎn)分別為![]() ,
,![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 與
與![]() 軸相切于點(diǎn)
軸相切于點(diǎn)![]() ,與
,與![]() 軸正半軸相交于
軸正半軸相交于![]() 、
、![]() 兩點(diǎn),且
兩點(diǎn),且![]() ,如圖1.
,如圖1.
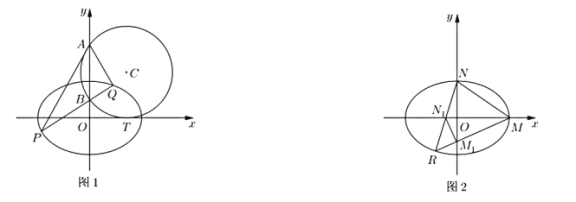
(1)求圓![]() 的方程;
的方程;
(2)如圖1,過(guò)點(diǎn)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點(diǎn),求證:射線
兩點(diǎn),求證:射線![]() 平分
平分![]() ;
;
(3)如圖2所示,點(diǎn)![]() 、
、![]() 是橢圓
是橢圓![]() 的兩個(gè)頂點(diǎn),且第三象限的動(dòng)點(diǎn)
的兩個(gè)頂點(diǎn),且第三象限的動(dòng)點(diǎn)![]() 在橢圓
在橢圓![]() 上,若直線
上,若直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,直線
,直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,試問:四邊形
,試問:四邊形![]() 的面積是否為定值?若是,請(qǐng)求出這個(gè)定值,若不是,請(qǐng)說(shuō)明理由.
的面積是否為定值?若是,請(qǐng)求出這個(gè)定值,若不是,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校高一年級(jí)模仿《中國(guó)詩(shī)詞大會(huì)》節(jié)目舉辦學(xué)校詩(shī)詞大會(huì),進(jìn)入正賽的條件為:電腦隨機(jī)抽取10首古詩(shī),參賽者能夠正確背誦6首及以上的進(jìn)入正賽,若學(xué)生甲參賽,他背誦每一首古詩(shī)的正確的概率均為![]()
(1)求甲進(jìn)入正賽的概率;
(2)若進(jìn)入正賽,則采用積分淘汰制,規(guī)則是:電腦隨機(jī)抽取4首古詩(shī),每首古詩(shī)背誦正確加2分,錯(cuò)誤減1分.由于難度增加,甲背誦每首古詩(shī)正確的概率為![]() ,求甲在正賽中積分
,求甲在正賽中積分![]() 的概率分布列及數(shù)學(xué)期望.
的概率分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求![]() 的圖像在
的圖像在![]() 處的切線方程;
處的切線方程;
(2)求函數(shù)![]() 的極大值;
的極大值;
(3)若![]() 對(duì)
對(duì)![]() 恒成立,求實(shí)數(shù)a的取值范圍.
恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)證明:![]() ;
;
(2)設(shè)![]() ,
,![]() 在
在![]() 上的極值點(diǎn)從小到大排列為
上的極值點(diǎn)從小到大排列為![]() ,求證:
,求證:![]() 時(shí),
時(shí),![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,點(diǎn)
是菱形,點(diǎn)![]() 在線段
在線段![]() 上,
上,![]() ,
,![]() 是線段
是線段![]() 的中點(diǎn),且三棱錐
的中點(diǎn),且三棱錐![]() 的體積是四棱錐
的體積是四棱錐![]() 體積的
體積的![]() .
.
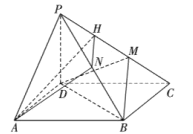
(1)若![]() 是
是![]() 的中點(diǎn),證明:平面
的中點(diǎn),證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是某小區(qū)2017年1月至2018年1月當(dāng)月在售二手房均價(jià)(單位:萬(wàn)元/平方米)的散點(diǎn)圖.(圖中月份代碼1—13分別對(duì)應(yīng)2017年1月—2018年1月)
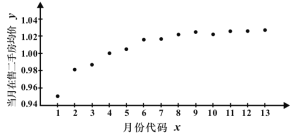
由散點(diǎn)圖選擇![]() 和
和![]() 兩個(gè)模型進(jìn)行擬合,經(jīng)過(guò)數(shù)據(jù)處理得到兩個(gè)回歸方程分別為
兩個(gè)模型進(jìn)行擬合,經(jīng)過(guò)數(shù)據(jù)處理得到兩個(gè)回歸方程分別為![]() 和
和![]() ,并得到以下一些統(tǒng)計(jì)量的值:
,并得到以下一些統(tǒng)計(jì)量的值:
|
| |
殘差平方和 | 0.000591 | 0.000164 |
總偏差平方和 | 0.006050 | |
(1)請(qǐng)利用相關(guān)指數(shù)![]() 判斷哪個(gè)模型的擬合效果更好;
判斷哪個(gè)模型的擬合效果更好;
(2)某位購(gòu)房者擬于2018年6月份購(gòu)買這個(gè)小區(qū)![]() 平方米的二手房(欲
平方米的二手房(欲
購(gòu)房為其家庭首套房).若購(gòu)房時(shí)該小區(qū)所有住房的房產(chǎn)證均已滿2年但未滿5年,請(qǐng)你利用(1)中擬合效果更好的模型估算該購(gòu)房者應(yīng)支付的購(gòu)房金額.(購(gòu)房金額=房款+稅費(fèi);房屋均價(jià)精確到0.001萬(wàn)元/平方米)
附注:根據(jù)有關(guān)規(guī)定,二手房交易需要繳納若干項(xiàng)稅費(fèi),稅費(fèi)是按房屋的計(jì)稅價(jià)格進(jìn)行征收.(計(jì)稅價(jià)格=房款),征收方式見下表:
契稅 (買方繳納) | 首套面積90平方米以內(nèi)(含90平方米)為1%;首套面積90平方米以上且144平方米以內(nèi)(含144平方米)為1.5%;面積144平方米以上或非首套為3% |
增值稅 (賣方繳納) | 房產(chǎn)證未滿2年或滿2年且面積在144平方米以上(不含144平方米)為5.6%;其他情況免征 |
個(gè)人所得稅 (賣方繳納) | 首套面積144平方米以內(nèi)(含144平方米)為1%;面積144平方米以上或非首套均為1.5%;房產(chǎn)證滿5年且是家庭唯一住房的免征 |
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . 參考公式:相關(guān)指數(shù)
. 參考公式:相關(guān)指數(shù)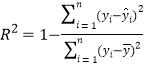 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】給定函數(shù)![]() 、
、![]() ,定義
,定義![]() .
.
(1)證明:![]() ;
;
(2)若![]() ,
,![]() ,證明:
,證明:![]() 是周期函數(shù);
是周期函數(shù);
(3)若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,證明:
,證明:![]() 是周期函數(shù)的充要條件是
是周期函數(shù)的充要條件是![]() 為有理數(shù).
為有理數(shù).
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com