
 (a∈R).
(a∈R). 時,
時,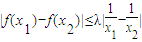 ,求λ的取值范圍.
,求λ的取值范圍.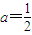 ,
,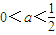 ,
,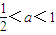 ,a≥1五種情況分別討論,最后綜合討論結果,即可得到f(x)的單調性;
,a≥1五種情況分別討論,最后綜合討論結果,即可得到f(x)的單調性;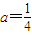 時,f(x)在(0,1)上是減函數(shù),在(1,2)上是增函數(shù),則f(x1)≥g(x2),可轉化為
時,f(x)在(0,1)上是減函數(shù),在(1,2)上是增函數(shù),則f(x1)≥g(x2),可轉化為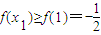 ≥f(x2),由g(x)=x2-2bx+4,我們易由函數(shù)恒成立問題的處理方法,求出滿足條件的實數(shù)b取值范圍.
≥f(x2),由g(x)=x2-2bx+4,我們易由函數(shù)恒成立問題的處理方法,求出滿足條件的實數(shù)b取值范圍.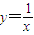 在(1,2]是減函數(shù),則
在(1,2]是減函數(shù),則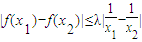 等價于
等價于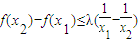 ,構造函數(shù)
,構造函數(shù) ,可得函數(shù)h(x)是減函數(shù),根據(jù)h'(x)≤0在(1,2]上恒成立,可構造關于λ的不等式,解不等式即可得到答案.
,可得函數(shù)h(x)是減函數(shù),根據(jù)h'(x)≤0在(1,2]上恒成立,可構造關于λ的不等式,解不等式即可得到答案. ,
,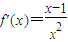 ,令
,令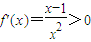 得x>1,
得x>1,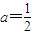 時,
時,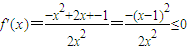 ,所以此時函數(shù)f(x)在(0,+∞)是減函數(shù);
,所以此時函數(shù)f(x)在(0,+∞)是減函數(shù);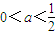 時,令
時,令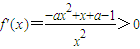 ,解得
,解得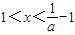 ,
,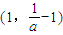 是增函數(shù),在
是增函數(shù),在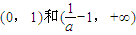 上是減函數(shù);----------------------------------------------(4分)
上是減函數(shù);----------------------------------------------(4分)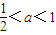 ,令
,令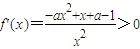 ,解得
,解得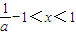 ,
,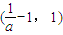 是增函數(shù),在
是增函數(shù),在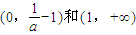 上是減函數(shù);-----------------------------------------(6分)
上是減函數(shù);-----------------------------------------(6分)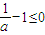 ,令
,令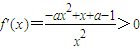 ,解得0<x<1,
,解得0<x<1,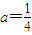 時,f(x)在(0,1)上是減函數(shù),在(1,2)上是增函數(shù),所以對任意x1∈(0,2),
時,f(x)在(0,1)上是減函數(shù),在(1,2)上是增函數(shù),所以對任意x1∈(0,2),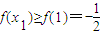 ,又已知存在x2∈[1,2],使f(x1)≥g(x2),所以
,又已知存在x2∈[1,2],使f(x1)≥g(x2),所以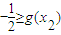 ,x2∈[1,2],
,x2∈[1,2],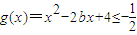 ,即
,即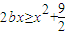 ,即
,即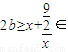
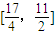 ,
,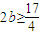 ,解得
,解得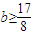 ,即實數(shù)b取值范圍是
,即實數(shù)b取值范圍是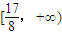 .--------------------(12分)
.--------------------(12分)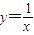 在(1,2]是減函數(shù),
在(1,2]是減函數(shù), 等價于
等價于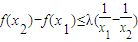 ,
,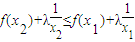
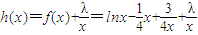 是減函數(shù),
是減函數(shù),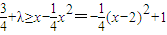 ,解得
,解得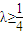 .---------(16分)
.---------(16分)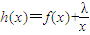 ,進而根據(jù)函數(shù)h(x)是減函數(shù),則h'(x)≤0在(1,2]上恒成立,構造關于λ的不等式.
,進而根據(jù)函數(shù)h(x)是減函數(shù),則h'(x)≤0在(1,2]上恒成立,構造關于λ的不等式. 

 名題金卷系列答案
名題金卷系列答案 優(yōu)加精卷系列答案
優(yōu)加精卷系列答案科目:高中數(shù)學 來源:2012-2013學年北京市十一學校高三(上)第四次月考數(shù)學試卷(理科)(解析版) 題型:解答題
 (a∈R且a≠0).
(a∈R且a≠0).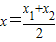 ;②曲線C在M處的切線平行于直線AB,則稱函數(shù)F(x)存在“中值相依切線”.
;②曲線C在M處的切線平行于直線AB,則稱函數(shù)F(x)存在“中值相依切線”.查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年江西省百所重點高中高三(上)段考數(shù)學試卷(理科)(解析版) 題型:解答題
 (a∈R且a≠0).
(a∈R且a≠0). ;②曲線C在M處的切線平行于直線AB,則稱函數(shù)F(x)存在“中值相依切線”.
;②曲線C在M處的切線平行于直線AB,則稱函數(shù)F(x)存在“中值相依切線”.查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年江蘇省常州高級中學高三(上)12月月考數(shù)學試卷(理科)(解析版) 題型:解答題
 (a∈R且a≠0).
(a∈R且a≠0). ;②曲線C在M處的切線平行于直線AB,則稱函數(shù)F(x)存在“中值相依切線”.
;②曲線C在M處的切線平行于直線AB,則稱函數(shù)F(x)存在“中值相依切線”.查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年甘肅省天水一中高一(下)第二次段考數(shù)學試卷(解析版) 題型:解答題
 ,a∈R.
,a∈R. 上的任意一個x,都有f(x)≤1成立,求a的取值范圍.
上的任意一個x,都有f(x)≤1成立,求a的取值范圍.查看答案和解析>>
科目:高中數(shù)學 來源:2013屆廣東省梅州市高二第二學期3月月考理科數(shù)學試卷 題型:解答題
已知函數(shù) (a∈R).
(a∈R).
(1)若 在[1,e]上是增函數(shù),求a的取值范圍;
在[1,e]上是增函數(shù),求a的取值范圍;
(2)若a=1,1≤x≤e,證明: <
< .
.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com