
如圖,已知矩形ABCD,SA⊥平面ABCD,且AE⊥SB于E,EF⊥SC于F.
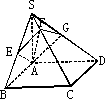
(1)求證:AF⊥SC;
(2)若平面AEF交SD于點G.求證:AG⊥SD.
|
分析:本題是證線線垂直的問題,可通過證線面垂直來實現. 證明:(1)因為SA⊥平面ABCD,BC 所以SA⊥BC. 因為四邊形ABCD是矩形, 所以AB⊥BC. 又SA∩AB=A,所以BC⊥平面SAB. 因為AE 又因為AE⊥SB,且SB∩BC=B, 所以AE⊥平面SBC,所以AE⊥SC. 又EF⊥SC,且EF∩AE=E, 所以SC⊥平面AEF,所以AF⊥SC. (2)因為SA⊥平面ABCD,所以SA⊥DC. 又AD⊥DC,且SA∩AD=A, 所以DC⊥平面SAD. 因為AG 由(1)有SC⊥平面AEF,AG 所以SC⊥AG. 又SC∩DC=C,所以AG⊥平面SDC. 因為SD 點評:無論是線面垂直還是面面垂直,都源于線與線的垂直,這種“降維”的思想方法,在解題時非常重要.在處理實際問題的過程中,可以先從題設條件入手,分析已有的垂直關系,再從結論入手,分析所要證明的垂直關系,從而架起已知與未知之間的橋梁. |


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:名師指點學高中課程 數學 高二(下) 題型:044
如圖,已知在矩形ABCD中,AB=3,BC=4,沿對角線AC將△ABC折起,使B點在平面ADC內的射影恰好落在AD上,求:
(1)異面直線AB與CD成的角;
(2)異面直線AB與CD的距離;
(3)二面角B-AC-D的大小.

查看答案和解析>>
科目:高中數學 來源:2014屆安徽省高一下學期期中考試數學試卷(解析版) 題型:解答題
如圖,已知矩形ABCD所在平面外一點P,PA⊥平面ABCD,E、F分別是AB、
PC的中點.
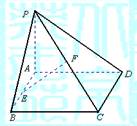
(1)求證:EF∥平面PAD;
(2)求證:EF⊥CD;
(3)若ÐPDA=45°求EF與平面ABCD所成的角的大小.
【解析】本試題主要考查了線面平行和線線垂直的運用,以及線面角的求解的綜合運用
第一問中,利用連AC,設AC中點為O,連OF、OE在△PAC中,∵ F、O分別為PC、AC的中點 ∴ FO∥PA …………①在△ABC中,∵ E、O分別為AB、AC的中點 ∴ EO∥BC ,又 ∵ BC∥AD ∴ EO∥AD …………②綜合①、②可知:平面EFO∥平面PAD∵ EF Ì 平面EFO ∴ EF∥平面PAD.
第二問中在矩形ABCD中,∵ EO∥BC,BC⊥CD ∴ EO⊥CD 又 ∵ FO∥PA,PA⊥平面AC ∴ FO⊥平面AC∴ EO為EF在平面AC內的射影 ∴ CD⊥EF.
第三問中,若ÐPDA=45°,則 PA=AD=BC ∵
EO
 BC,FO
BC,FO
 PA
PA
∴ FO=EO 又∵ FO⊥平面AC∴ △FOE是直角三角形 ∴ ÐFEO=45°
證:連AC,設AC中點為O,連OF、OE(1)在△PAC中,∵ F、O分別為PC、AC的中點∴ FO∥PA …………① 在△ABC中,∵ E、O分別為AB、AC的中點 ∴ EO∥BC ,又 ∵ BC∥AD ∴ EO∥AD …………②綜合①、②可知:平面EFO∥平面PAD
∵ EF Ì 平面EFO ∴ EF∥平面PAD.
(2)在矩形ABCD中,∵ EO∥BC,BC⊥CD∴ EO⊥CD 又 ∵ FO∥PA,PA⊥平面AC ∴ FO⊥平面AC ∴ EO為EF在平面AC內的射影 ∴ CD⊥EF.
(3)若ÐPDA=45°,則 PA=AD=BC ∵ EO
 BC,FO
BC,FO
 PA
PA
∴ FO=EO 又 ∵ FO⊥平面AC ∴ △FOE是直角三角形 ∴ ÐFEO=45°

查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省南京市高三第二次模擬考試數學卷 題型:解答題
在A、B、C、D四小題中只能選做2題,每小題10,共計20分。請在答題卡指定區域作答。解答應寫出文字說明、證明過程或演算步驟。
A、選修4-1:幾何證明選講
如圖,已知梯形ABCD為圓內接四邊形,AD//BC,過C作該圓的切線,交AD的延長線于E,求證:ΔABC∽ΔEDC。

B、選修4-2:矩形與變換
已知 為矩陣
為矩陣 屬于λ的一個特征向量,求實數a,λ的值及A2。
屬于λ的一個特征向量,求實數a,λ的值及A2。
C、選修4-4:坐標系與參數方程
在平面直角坐標系xoy中,曲線C的參數方程為 (α為參數),曲線D的參數方程為
(α為參數),曲線D的參數方程為 ,(t為參數)。若曲線C、D有公共點,求實數m的取值范圍。
,(t為參數)。若曲線C、D有公共點,求實數m的取值范圍。
D、選修4-5:不等式選講
已知a,b都是正實數,且ab=2。求證:(1+2a)(1+b)≥9。
查看答案和解析>>
科目:高中數學 來源: 題型:
如圖,已知幾何體ABC-DEF中,△ABC及△DEF都是邊長為2的等邊三角形,四邊形ABEF為矩形,且CD=AF+2,CD//AF,O為AB中點.
(1)求證:AB⊥平面DCO
(2)若M為CD中點,AF=x,則當x取何值時,使AM與平面ABEF所成角為45°?
試求相應的x值的.
(3)求該幾何體在(2)的條件下的體積.

查看答案和解析>>
科目:高中數學 來源:2011屆江蘇省南京市高三第二次模擬考試數學卷 題型:解答題
在A、B、C、D四小題中只能選做2題,每小題10,共 計20分。請在答題卡指定區域作答。解答應寫出文字
計20分。請在答題卡指定區域作答。解答應寫出文字 說明、證明過程或演算
說明、證明過程或演算 步驟。
步驟。
A、選修4-1:幾何證明選講
如圖,已知梯形ABCD為 圓內接四邊形,AD//BC,過C作該圓的切線,交AD的延長線于E,求證:ΔABC∽ΔEDC。
圓內接四邊形,AD//BC,過C作該圓的切線,交AD的延長線于E,求證:ΔABC∽ΔEDC。
B、選修4-2:矩形與變換
已知 為矩陣
為矩陣 屬于λ的一個特征向量,求實數a,λ的值及A2。
屬于λ的一個特征向量,求實數a,λ的值及A2。
C、選修4-4:坐標系與參數方程 在平面直角坐標系xoy中,曲線C的參數方程為
在平面直角坐標系xoy中,曲線C的參數方程為 (α為參數),曲線D的參數方程為
(α為參數),曲線D的參數方程為 ,(t為參數)。若曲線C、D有公共點,求實數m的取值范圍。
,(t為參數)。若曲線C、D有公共點,求實數m的取值范圍。
D、選修4-5:不等式選講
已知a,b都是 正實數,且ab=2。求證:(1+2a)(1+b)≥9。
正實數,且ab=2。求證:(1+2a)(1+b)≥9。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com