
(本小題12分)某鄉鎮為了盤活資本,優化組合,決定引進資本拯救出現嚴重虧損的企業。長年在外經商的王先生為了回報家鄉,決定投資線路板廠和機械加工廠。王先生經過預算,如果引進新技術在優化管理的情況下,線路板廠和機械加工廠可能的最大盈利率分別為95﹪和80﹪,可能的最大虧損率分別為30﹪和10﹪。由于金融危機的影響,王先生決定最多出資100萬元引進新技術,要求確保可能的資金虧損不超過18萬元.問王先生對線路板廠和機械加工廠各投資多少萬元,才能使可能的盈利最大?
思路點撥:這是一個實際生活中的最優化問題,可根據條件列出線性約束條件和目標函數,畫出可行域求解。
解:設王先生分別用x萬元、y萬元投資線路板廠和機械加工廠兩個項目,
盈利為z萬元。
由題意知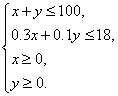 -------------------3分
-------------------3分
目標函數![]() -------------------4分
-------------------4分
上述不等式組表示的平面區域如圖所示,陰影部分(含邊界)即可行域.
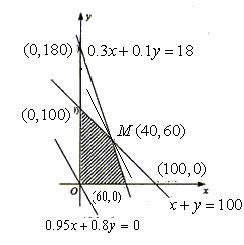 ----------------------7分
----------------------7分
作直線![]() ,并作平行于直線
,并作平行于直線![]() 的一組直線
的一組直線![]()
與可行域相交,其中有一條直線經過可行域上的M點,
且與直線![]() 的距離最大,
的距離最大,
這里M點是直線![]() 和
和![]() 的交點.-----------9分
的交點.-----------9分
解方程組![]() 得x=40,y=60
得x=40,y=60
此時![]() (萬元).
(萬元).
所以當x=40,y=60時z取得最大值. --------11分
答:王先生用40萬元投資線路板廠、60萬元機械加工廠,才能在確保虧損不超過18萬元的前提下,使可能的盈利最大為86萬元。 ---------------12分
命題意圖:本題考查了線性規劃知識,利用線性規劃知識解決實際生活中的最優化問題。


科目:高中數學 來源: 題型:
(本小題12分) 某中學在高一開設了4門選修課,每個學生必須且只需選修1門選修課,對于該年級的甲、乙、丙3名學生,回答下列問題。 (I)求這3名學生選擇的選修課互不相同的概率; (II)求恰有2門選修課沒有被這3名學生選擇的概率;(III)某一選修課被這3名學生選擇的人數的數學期望。
查看答案和解析>>
科目:高中數學 來源:2011年云南省建水一中高一上學期期中考試數學 題型:解答題
(本小題12分)
某企業為適應市場需求,準備投入資金16萬元生產W和R型兩種產品。經市場預測,生產W型產品所獲利潤 (萬元)與投入資金
(萬元)與投入資金 (萬元)成正比例關系,且當投入資金為6萬元時,可獲利潤1.5
(萬元)成正比例關系,且當投入資金為6萬元時,可獲利潤1.5 萬元。生產R型產品所獲利潤
萬元。生產R型產品所獲利潤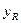 (萬元)與投入資金
(萬元)與投入資金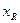 (
( 萬元)滿足關系
萬元)滿足關系 ,為獲得最大總利潤,問生產W、R型產品各應投入資金多少萬元?獲得的最大總利潤是多少?
,為獲得最大總利潤,問生產W、R型產品各應投入資金多少萬元?獲得的最大總利潤是多少?
查看答案和解析>>
科目:高中數學 來源:2014屆福建省高二上學期期中考試文科數學試題(解析版) 題型:解答題
(本小題12分)某工廠有工人1000名,其中250名工人參加過短期培訓(稱為A類工人),另外750名工人參加過長期培訓(稱為B類工人).現用分層抽樣方法(按A類,B類分二層)從該工廠的工人中共抽查100名工人,調查他們的生產能力(生產能力指一天加工的零件數).從A類工人中抽查結果和從B類工人中的抽查結果分別如下表1和表2
表1:
|
生產能力分組 |
|
|
|
|
|
|
人數 |
4 |
8 |
|
5 |
3 |
表2:
|
生產能力分組 |
|
|
|
|
|
人數 |
6 |
y |
36 |
18 |
(1)先確定 ,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)(注意:本題請在答題卡上作圖)
,再在答題紙上完成下列頻率分布直方圖。就生產能力而言,A類工人中個體間的差異程度與B類工人中個體間的差異程度哪個更小?(不用計算,可通過觀察直方圖直接回答結論)(注意:本題請在答題卡上作圖)

(2)分別估計 類工人和
類工人和 類工人生產能力的眾數、中位數和平均數。(精確到0.1)
類工人生產能力的眾數、中位數和平均數。(精確到0.1)
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題12分)
某企業為適應市場需求,準備投入資金16萬元生產W和R型兩種產品。經市場預測,生產W型產品所獲利潤![]() (萬元)與投入資金
(萬元)與投入資金![]() (萬元)成正比例關系,且當投入資金為6萬元時,可獲利潤1.5萬元。生產R型產品所獲利潤
(萬元)成正比例關系,且當投入資金為6萬元時,可獲利潤1.5萬元。生產R型產品所獲利潤![]() (萬元)與投入資金
(萬元)與投入資金![]() (萬元)滿足關系
(萬元)滿足關系![]() ,為獲得最大總利潤,問生產W、R型產品各應投入資金多少萬元?獲得的最大總利潤是多少?
,為獲得最大總利潤,問生產W、R型產品各應投入資金多少萬元?獲得的最大總利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com