
【題目】已知O為![]() 內一點,若分別滿足①
內一點,若分別滿足①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (其中
(其中![]() 為
為![]() 中,角
中,角![]() 所對的邊).則O依次是
所對的邊).則O依次是![]() 的( )
的( )
A.內心、重心、垂心、外心B.外心、垂心、重心、內心
C.外心、內心、重心、垂心D.內心、垂心、外心、重心
科目:高中數學 來源: 題型:
【題目】某地區高考實行新方案,規定:語文、數學和英語是考生的必考科目,考生還須從物理、化學、生物、歷史、地理和政治六個科目中選取三個科目作為選考科目.若一個學生從六個科目中選出了三個科目作為選考科目,則稱該學生的選考方案確定;否則,稱該學生選考方案待確定.例如,學生甲選擇“物理、化學和生物”三個選考科目,則學生甲的選考方案確定,“物理、化學和生物”為其選考方案.
某學校為了解高一年級420名學生選考科目的意向,隨機選取30名學生進行了一次調查,統計選考科目人數如下表:
性別 | 選考方案確定情況 | 物理 | 化學 | 生物 | 歷史 | 地理 | 政治 | |||||||||
男生 | 選考方案確定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 | |||||||||
選考方案待確定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | ||||||||||
女生 | 選考方案確定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 | |||||||||
選考方案待確定的有6人 | 5 | 4 | 1 | 0 | 0 | 求 |
年份 | 5 | 6 | 7 | 8 |
投資金額 | 15 | 17 | 21 | 27 |
(1)利用所給數據,求出投資金額![]() 與年份
與年份![]() 之間的回歸直線方程
之間的回歸直線方程![]() ;
;
(2)預測該社區在2019年在“文化丹青”上的投資金額.
(附:對于一組數據![]() ,
, ![]() ,…,
,…, ![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為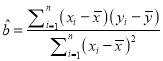 ,
, ![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.互相垂直的兩條直線的直觀圖仍然是互相垂直的兩條直線
B.梯形的直觀圖可能是平行四邊形
C.矩形的直觀圖可能是梯形
D.正方形的直觀圖可能是平行四邊形
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,圓![]() :
:![]() .
.

(Ⅰ)若圓C與x軸相切,求圓C的方程;
(Ⅱ)已知![]() ,圓
,圓![]() 與x軸相交于兩點
與x軸相交于兩點![]() (點
(點![]() 在點
在點![]() 的左側).過點
的左側).過點![]() 任作一條直線與圓
任作一條直線與圓![]() :
:![]() 相交于兩點A,B.問:是否存在實數a,使得
相交于兩點A,B.問:是否存在實數a,使得![]() =
=![]() ?若存在,求出實數a的值,若不存在,請說明理由.
?若存在,求出實數a的值,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com