Question

如圖，若執行程序框圖，則輸出的結果是    ．

Answer 1

【答案】分析：首先分析程序框圖，循環體為“當型”循環結構，按照循環結構進行運算，求出滿足題意時的n．
解答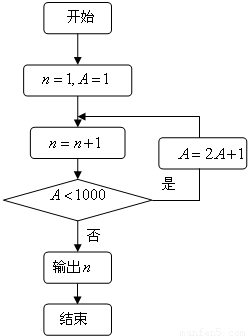：解：根據題意，本程序框圖為求n的值，
循環體為“當型”循環結構．
第一次循環：n=1+1=2，A=2×1+1=3；
第二次循環：n=2+1=3，A=2×3+1=7；
第三次循環：n=3+1=4，A=2×7+1=15；
第四次循環：n=4+1=5，A=2×15+1=31；
第五次循環：n=5+1=6，A=2×31+1=63；
第六次循環：n=6+1=7，A=2×63+1=127；
第七次循環：n=7+1=8，A=2×127+1=255；
第八次循環：n=8+1=9，A=2×255+1=511；
第九次循環：n=9+1=10，A=2×511+1=1023；
第十次循環：n=10+1=11，
∵A=1023＞1000，
∴結束循環，輸出n=11．
故答案為：11．
點評：本題為程序框圖題，考查對循環結構的理解和認識，按照循環結構運算后得出結果．屬于基礎題．