
【題目】正五邊形![]() 的對角線
的對角線![]() 分別與對角線
分別與對角線![]() 、
、![]() 交于點
交于點![]() 、
、![]() ,對角線
,對角線![]() 分別與對角線
分別與對角線![]() 、
、![]() 交于點
交于點![]() 、
、![]() ,對角線
,對角線![]() 與對角線
與對角線![]() 交于點
交于點![]() . 設由圖2中的10個點
. 設由圖2中的10個點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和線段構成的等腰三角形的集合為
和線段構成的等腰三角形的集合為![]() .
.
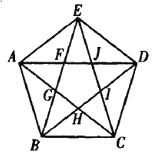
(1)求![]() 中元素的數目;
中元素的數目;
(2)若將這10個點中的每個點任意染為紅、藍兩種顏色之一,問是否一定存在![]() 中的一個等腰三角形,其三個頂點同色?
中的一個等腰三角形,其三個頂點同色?
(3)若將這10個點中的任意![]() 個點染為紅色,使得一定存在
個點染為紅色,使得一定存在![]() 中的一個等腰三角形,其三個頂點同為紅色,求
中的一個等腰三角形,其三個頂點同為紅色,求![]() 的最小值.
的最小值.
【答案】(1)35;(2)見解析;(3)6.
【解析】
(1)因為由圖2中的10個點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和線段構成的三角形均為等腰三角形,所以,
和線段構成的三角形均為等腰三角形,所以,![]() .
.
(2)由抽屜原則,知![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中一定有三個點同色,且這三個點構成的三角形屬于
中一定有三個點同色,且這三個點構成的三角形屬于![]() ,故一定存在
,故一定存在![]() 中的等腰三角形,其三個頂點同色.
中的等腰三角形,其三個頂點同色.
(3)若![]() ,則將
,則將![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 染為紅色,于是,不存在屬于
染為紅色,于是,不存在屬于![]() 的頂點同為紅色的三角形.
的頂點同為紅色的三角形.
若![]() ,當
,當![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中有不少于三個紅點時,一定存在屬于
中有不少于三個紅點時,一定存在屬于![]() 且頂點同為紅色的三角形;當
且頂點同為紅色的三角形;當![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中不少于三個紅點時,
中不少于三個紅點時,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中至少有四個紅點.
中至少有四個紅點.
若![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中恰有四個紅點,不妨假設
中恰有四個紅點,不妨假設![]() 、
、![]() 、
、![]() 、
、![]() 為紅點,則
為紅點,則![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中至少有兩個紅點,不妨假設
中至少有兩個紅點,不妨假設![]() 的紅點,則
的紅點,則![]() 是屬于
是屬于![]() 且頂點同為紅色的三角形;否則,
且頂點同為紅色的三角形;否則,![]() 、
、![]() 同為紅色,于是,
同為紅色,于是,![]() 是屬于
是屬于![]() 且頂點間同為紅色的三角形.
且頂點間同為紅色的三角形.
因此,![]() 的最小值為6.
的最小值為6.


科目:高中數學 來源: 題型:
【題目】一個大于1的自然數,除了1和它本身外,不能被其他自然數整除,則稱這個數為質數.質數的個數是無窮的.設由所有質數組成的無窮遞增數列![]() 的前
的前![]() 項和為
項和為![]() ,等差數列1,3,5,7,…中所有不大于
,等差數列1,3,5,7,…中所有不大于![]() 的項的和為
的項的和為![]() .
.
(Ⅰ)求![]() 和
和![]() ;
;
(Ⅱ)判斷![]() 和
和![]() 的大小,不用證明;
的大小,不用證明;
(Ⅲ)設![]() ,求證:
,求證:![]() ,
,![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線![]() 的焦點
的焦點![]() 且斜率為1的直線與拋物線
且斜率為1的直線與拋物線![]() 交于
交于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)點![]() 是拋物線
是拋物線![]() 上異于
上異于![]() 、
、![]() 的任意一點,直線
的任意一點,直線![]() 、
、![]() 與拋物線
與拋物線![]() 的準線分別交于點
的準線分別交于點![]() 、
、![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知從![]() 地到
地到![]() 地有兩條道路可以到達,走道路①準點到達的概率為
地有兩條道路可以到達,走道路①準點到達的概率為![]() ,不準點到達的概率為
,不準點到達的概率為![]() ;走道路②準點到達的概率為
;走道路②準點到達的概率為![]() ,不準點到達的概率為
,不準點到達的概率為![]() .若甲乙兩車走道路①,丙車由于其他原因走道路②,且三輛車是否準點到達相互之間沒有影響.
.若甲乙兩車走道路①,丙車由于其他原因走道路②,且三輛車是否準點到達相互之間沒有影響.
(1)若三輛車中恰有一輛車沒有準點到達的概率為![]() ,求走道路②準點到達的概率
,求走道路②準點到達的概率![]() ;
;
(2)在(1)的條件下,求三輛車中準點到達車輛的輛數的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】算籌是在珠算發明以前我國獨創并且有效的計算工具,為我國古代數學的發展做出了很大貢獻.在算籌計數法中,以“縱式”和“橫式”兩種方式來表示數字,如圖:

表示多位數時,個位用縱式,十位用橫式,百位用縱式,千位用橫式,以此類推,遇零則置空,如圖:
![]()
如果把5根算籌以適當的方式全部放入 下面的表格中,那么可以表示的三位數的個數為( )
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位,再把圖象上所有點的橫坐標縮短到原來的
個單位,再把圖象上所有點的橫坐標縮短到原來的![]() 倍(縱坐標不變),得到
倍(縱坐標不變),得到![]() 的圖象,則關于
的圖象,則關于![]() 的圖象,下列結論不正確的是
的圖象,下列結論不正確的是
A. 周期為![]() B. 關于點
B. 關于點![]() 對稱
對稱
C. 在![]() 單調遞增 D. 在
單調遞增 D. 在![]() 單調遞減
單調遞減
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在全面抗擊新冠肺炎疫情這一特殊時期,我市教育局提出“停課不停學”的口號,鼓勵學生線上學習.某校數學教師為了調查高三學生數學成績與線上學習時間之間的相關關系,在高三年級中隨機選取![]() 名學生進行跟蹤問卷,其中每周線上學習數學時間不少于
名學生進行跟蹤問卷,其中每周線上學習數學時間不少于![]() 小時的有
小時的有![]() 人,在這
人,在這![]() 人中分數不足
人中分數不足![]() 分的有
分的有![]() 人;在每周線上學習數學時間不足于
人;在每周線上學習數學時間不足于![]() 小時的人中,在檢測考試中數學平均成績不足
小時的人中,在檢測考試中數學平均成績不足![]() 分的占
分的占![]() .
.
(1)請完成![]() 列聯表;并判斷是否有
列聯表;并判斷是否有![]() 的把握認為“高三學生的數學成績與學生線上學習時間有關”;
的把握認為“高三學生的數學成績與學生線上學習時間有關”;
分數不少于 | 分數不足 | 合計 | |
線上學習時間不少于 | |||
線上學習時間不足 | |||
合計 |
(2)在上述樣本中從分數不足于![]() 分的學生中,按照分層抽樣的方法,抽到線上學習時間不少于
分的學生中,按照分層抽樣的方法,抽到線上學習時間不少于![]() 小時和線上學習時間不足
小時和線上學習時間不足![]() 小時的學生共
小時的學生共![]() 名,若在這
名,若在這![]() 名學生中隨機抽取
名學生中隨機抽取![]() 人,求這
人,求這![]() 人每周線上學習時間都不足
人每周線上學習時間都不足![]() 小時的概率.(臨界值表僅供參考)
小時的概率.(臨界值表僅供參考)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考公式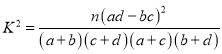 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com