已知經過點A(-2,0),且以(λ,1+λ)為方向向量的直線l1與經過點B(2,0),且以(1+λ,-3λ)為方向向量的直線l2相交于點P,其中λ∈R.
(1)求點P的軌跡C的方程;
(2)是否存在直線l:y=kx+m(m≠0)與軌跡C相交于不同的兩點M、N,且滿足|BM|=|BN|?若存在,求出m的取值范圍;若不存在,請說明理由.
【答案】
分析:(1)對λ進行討論,即可求點P的軌跡C的方程;
(2)假設存在直線l:y=kx+m(m≠0)與軌跡C相交于不同的兩點M、N,且滿足|BM|=|BN|,求出線段MN的中點M
的坐標,利用M
在橢圓C的內部,在直線l上,即可求得結論.
解答:解:(1)當λ≠0且λ≠-1時,直線l
1:
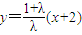
,直線l
2:y=
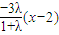
消參可得
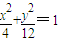
①
當λ=0時,直線l
1:x=-2,直線l
2:y=0,其交點為(-2,0),適合①;
當λ=-1時,直線l
1:y=0,直線l
2:x=2,其交點為(2,0),適合①;
∴點P的軌跡C的方程為
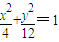
;
(2)假設存在直線l:y=kx+m(m≠0)與軌跡C相交于不同的兩點M(x
1,y
1),N(x
2,y
2),且滿足|BM|=|BN|.
令線段MN的中點M
(x
,y
),則BM
垂直平分MN
∵
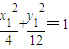
,
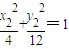
,
∴兩式相減可得,
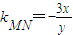
=k②
∵BM
⊥MN,∴

③
由②③可得
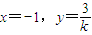
∴M
(-1,
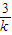
)
∵M
在橢圓C的內部,故

∴|k|>1
∵M
(-1,
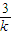
)在直線l上,
∴
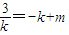
,
∴|m|=|k+
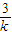
|≥
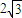
,當且僅當|k|=
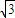
時取等號
∴存在直線l滿足條件,此時m的取值范圍為(-∞,-
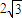
)∪(
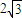
,+∞).
點評:本題考查軌跡方程,考查存在性問題的研究,考查學生分析解決問題的能力,屬于中檔題.

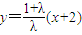 ,直線l2:y=
,直線l2:y=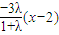
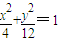 ①
①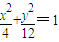 ;
;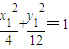 ,
,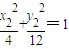 ,
,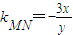 =k②
=k② ③
③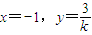
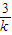 )
)
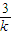 )在直線l上,
)在直線l上,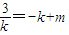 ,
,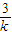 |≥
|≥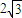 ,當且僅當|k|=
,當且僅當|k|=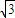 時取等號
時取等號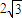 )∪(
)∪(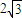 ,+∞).
,+∞).
