解:(Ⅰ)
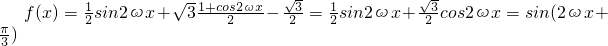
,-------(3分)
由題意知,最小正周期
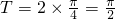
,又
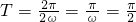
,所以ω=2,
∴
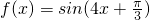
.-------------(6分)
(Ⅱ)將f(x)的圖象向右平移個

個單位后,得到 y=
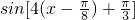
=
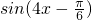
的圖象,
再將所得圖象所有點的橫坐標伸長到原來的2倍,縱坐標不變,得到
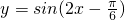
的圖象,

.---------(9分)
令
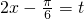
,∵
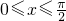
,∴

,g(x)+k=0,在區(qū)間

上有且只有一個實數(shù)解,
即函數(shù)y=g(x)與y=-k在區(qū)間

上有且只有一個交點,由正弦函數(shù)的圖象可知

或-k=1
∴
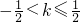
,或k=-1.--------(12分)
分析:(Ⅰ)利用三角函數(shù)的恒等變換把函數(shù)f(x)的解析式化為
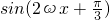
,根據(jù)周期求出ω=2,從而得到
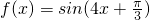
.
(Ⅱ)將f(x)的圖象向右平移個

個單位后,得到 y=
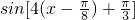
=
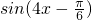
的圖象,再將所得圖象所有點的橫坐標伸長到原來的2倍得到
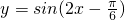
的圖象,可得
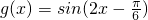
,函數(shù)y=g(x)與y=-k在區(qū)間

上有且只有一個交點,由正弦函數(shù)的圖象可得實數(shù)k的取值范圍.
點評:本題主要考查三角函數(shù)的恒等變換及化簡求值,三角函數(shù)的周期性和求法,y=Asin(ωx+∅)的圖象變換規(guī)律,屬于中檔題.

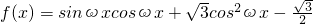 (ω>0),直線x=x1,x=x2是y=f(x)圖象的任意兩條對稱軸,且|x1-x2|的最小值為
(ω>0),直線x=x1,x=x2是y=f(x)圖象的任意兩條對稱軸,且|x1-x2|的最小值為 .
. 個單位后,再將得到的圖象上各點的橫坐標伸長為原來的2倍,縱坐標不變,得到函數(shù)y=g(x)的圖象,若關(guān)于x的方程g(x)+k=0,在區(qū)間
個單位后,再將得到的圖象上各點的橫坐標伸長為原來的2倍,縱坐標不變,得到函數(shù)y=g(x)的圖象,若關(guān)于x的方程g(x)+k=0,在區(qū)間 上有且只有一個實數(shù)解,求實數(shù)k的取值范圍.
上有且只有一個實數(shù)解,求實數(shù)k的取值范圍.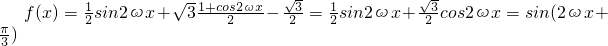 ,-------(3分)
,-------(3分)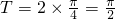 ,又
,又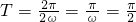 ,所以ω=2,
,所以ω=2,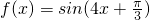 .-------------(6分)
.-------------(6分) 個單位后,得到 y=
個單位后,得到 y=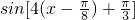 =
=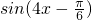 的圖象,
的圖象,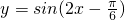 的圖象,
的圖象, .---------(9分)
.---------(9分)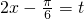 ,∵
,∵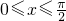 ,∴
,∴ ,g(x)+k=0,在區(qū)間
,g(x)+k=0,在區(qū)間 上有且只有一個實數(shù)解,
上有且只有一個實數(shù)解, 上有且只有一個交點,由正弦函數(shù)的圖象可知
上有且只有一個交點,由正弦函數(shù)的圖象可知 或-k=1
或-k=1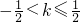 ,或k=-1.--------(12分)
,或k=-1.--------(12分)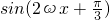 ,根據(jù)周期求出ω=2,從而得到
,根據(jù)周期求出ω=2,從而得到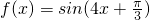 .
. 個單位后,得到 y=
個單位后,得到 y=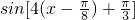 =
=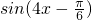 的圖象,再將所得圖象所有點的橫坐標伸長到原來的2倍得到
的圖象,再將所得圖象所有點的橫坐標伸長到原來的2倍得到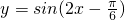 的圖象,可得
的圖象,可得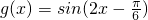 ,函數(shù)y=g(x)與y=-k在區(qū)間
,函數(shù)y=g(x)與y=-k在區(qū)間 上有且只有一個交點,由正弦函數(shù)的圖象可得實數(shù)k的取值范圍.
上有且只有一個交點,由正弦函數(shù)的圖象可得實數(shù)k的取值范圍.
