
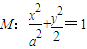
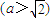 的右焦點為F1,直線
的右焦點為F1,直線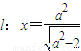 與x軸交于點A,若
與x軸交于點A,若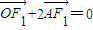 (其中O為坐標原點).
(其中O為坐標原點).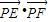 的最大值.
的最大值.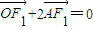 ,即可求得橢圓的方程;
,即可求得橢圓的方程;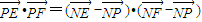 =
=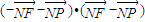 =
=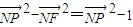 ,從而求
,從而求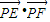 的最大值轉化為求
的最大值轉化為求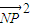 的最大值;
的最大值;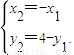
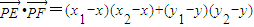 =
=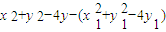 .根據點E在圓N上,點P在橢圓M上,可得
.根據點E在圓N上,點P在橢圓M上,可得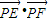 =
=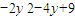 =
=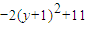 ,利用
,利用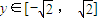 ,可求
,可求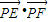 的最大值;
的最大值;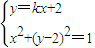 ,解得
,解得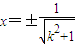 ,再分別求得
,再分別求得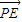 、
、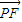 ,利用
,利用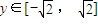 ,可求
,可求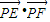 的最大值;②若直線EF的斜率不存在,此時EF的方程為x=0,同理可求
的最大值;②若直線EF的斜率不存在,此時EF的方程為x=0,同理可求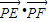 的最大值.
的最大值.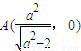 ,
,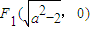 ,…(1分)
,…(1分)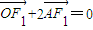 ,得
,得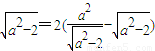 .…(3分)
.…(3分)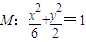 .…(4分)
.…(4分)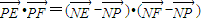 …(6分)
…(6分)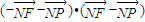 …(7分)
…(7分)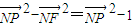 .…(8分)
.…(8分)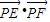 的最大值轉化為求
的最大值轉化為求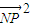 的最大值.…(9分)
的最大值.…(9分)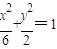 ,即
,即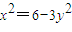 .…(11分)
.…(11分)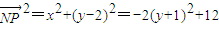 .…(12分)
.…(12分)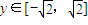 ,所以當y=-1時,
,所以當y=-1時,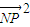 取得最大值12,…(13分)
取得最大值12,…(13分)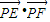 的最大值為11,…(14分)
的最大值為11,…(14分)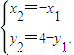 …(6分)
…(6分)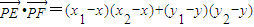 …(7分)=(x1-x)(-x1-x)+(y1-y)(4-y1-y)=
…(7分)=(x1-x)(-x1-x)+(y1-y)(4-y1-y)=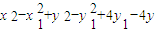 =
=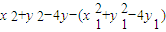 .…(9分)
.…(9分)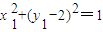 ,即
,即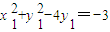 .…(10分)
.…(10分)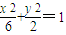 ,即
,即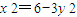 .…(11分)
.…(11分)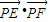 =
=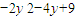 =
=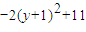 .…(12分)
.…(12分)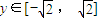 ,所以當y=-1時,
,所以當y=-1時,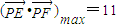 .…(14分)
.…(14分)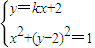 ,解得
,解得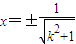 .…(7分)
.…(7分)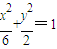 ,即
,即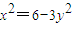 .…(8分)
.…(8分)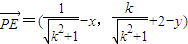 ,
,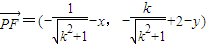 …(9分)
…(9分)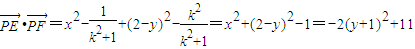 .…(10分)
.…(10分)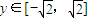 ,所以當y=-1時,
,所以當y=-1時,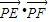 取得最大值11,…(11分)
取得最大值11,…(11分)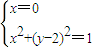 ,解得y=1或y=3.
,解得y=1或y=3.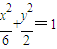 ,即
,即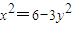 .
.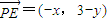 ,
,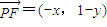 .
.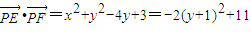 .
.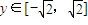 ,所以當y=-1時,
,所以當y=-1時,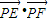 取得最大值11,…(13分)
取得最大值11,…(13分)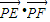 的最大值為11,…(14分)
的最大值為11,…(14分)

 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數學 來源:2012-2013學年江蘇省鹽城中學高三(上)第五次學情調研數學試卷(解析版) 題型:填空題
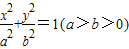 的右焦點為F1,右準線為l1,若過F1且垂直于x軸的弦長等于點F1到l1的距離,則橢圓的率心率是 .
的右焦點為F1,右準線為l1,若過F1且垂直于x軸的弦長等于點F1到l1的距離,則橢圓的率心率是 .查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省蘇州市高二(上)期末數學試卷(解析版) 題型:填空題
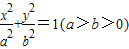 的右焦點為F1,右準線為l1,若過F1且垂直于x軸的弦長等于點F1到l1的距離,則橢圓的率心率是 .
的右焦點為F1,右準線為l1,若過F1且垂直于x軸的弦長等于點F1到l1的距離,則橢圓的率心率是 .查看答案和解析>>
科目:高中數學 來源:《圓錐曲線》2012-2013學年廣東省十三大市高三(上)期末數學試卷匯編(理科)(解析版) 題型:解答題
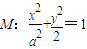
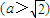 的右焦點為F1,直線
的右焦點為F1,直線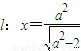 與x軸交于點A,若
與x軸交于點A,若 (其中O為坐標原點).
(其中O為坐標原點).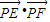 的最大值.
的最大值.查看答案和解析>>
科目:高中數學 來源:1999年全國統一高考數學試卷(理科)(解析版) 題型:解答題
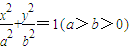 的右焦點為F1,右準線為l1,若過F1且垂直于x軸的弦長等于點F1到l1的距離,則橢圓的率心率是 .
的右焦點為F1,右準線為l1,若過F1且垂直于x軸的弦長等于點F1到l1的距離,則橢圓的率心率是 .查看答案和解析>>
科目:高中數學 來源:1999年廣東省高考數學試卷(解析版) 題型:解答題
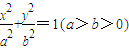 的右焦點為F1,右準線為l1,若過F1且垂直于x軸的弦長等于點F1到l1的距離,則橢圓的率心率是 .
的右焦點為F1,右準線為l1,若過F1且垂直于x軸的弦長等于點F1到l1的距離,則橢圓的率心率是 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com