
如圖,在四棱錐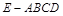 中,
中,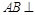 平面
平面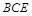 ,
,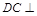 平面
平面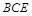 ,
,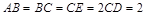 ,
,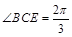 .
.
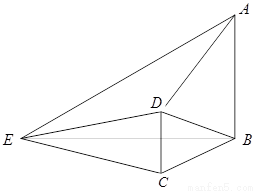
(Ⅰ)求證:平面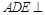 平面
平面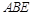 ;
;
(Ⅱ)求二面角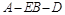 的大小.
的大小.
(Ⅰ)詳見解析;(Ⅱ)
【解析】
試題分析:(Ⅰ)根據兩個平面垂直的條件,在平面 內找到一條垂直于平面
內找到一條垂直于平面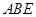 的直線即可,取
的直線即可,取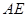 的中點
的中點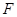 ,可證明
,可證明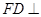 平面
平面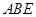 ;(Ⅱ) 二面角
;(Ⅱ) 二面角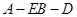 與二面角
與二面角 相等,二面角
相等,二面角 的平面角為
的平面角為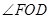 ,求出
,求出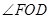 即可.(解法2采用的是向量的方法,求出平面
即可.(解法2采用的是向量的方法,求出平面 、
、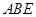 的法向量,即可證明平面
的法向量,即可證明平面 平面
平面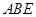 ;求出平面
;求出平面 、
、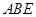 的法向量,即可求出二面角
的法向量,即可求出二面角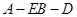 .)
.)
(Ⅰ)證明:取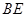 的中點
的中點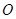 ,
,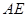 的中點
的中點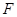 ,連
,連 ,
,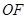 ,
, ,則
,則

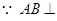 平面
平面 ,
, 平面
平面 ,∴
,∴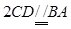 ,
,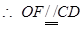
 是平行四邊形,
是平行四邊形,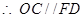 .
.
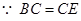 ,
,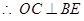 ,又
,又 平面
平面 .
.
 平面
平面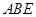 .
.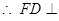 平面
平面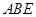 .
.
從而平面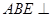 平面
平面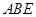 . 6分
. 6分
(Ⅱ)二面角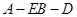 與二面角
與二面角 相等,
相等,
由(Ⅰ)知二面角 的平面角為
的平面角為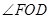 .
.
 ,
, ,
,
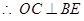 得
得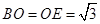 ,
,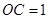 ,
,
 為正方形,
為正方形, ,
,
∴二面角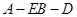 的大小為
的大小為 . 12分
. 12分
解法2:取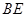 的中點
的中點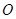 ,連
,連 .
.
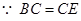 ,
,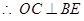 ,又
,又 平面
平面 .
.
以 為原點建立如圖空間直角坐標系
為原點建立如圖空間直角坐標系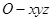 ,
,

則由已知條件有: 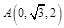 ,
,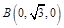 ,
,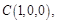

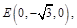
設平面 的法向量為
的法向量為 ,
,
則由
及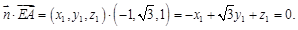
可取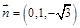
又 平面
平面 ,
,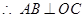 ,
,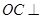 平面
平面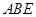 ,
,
∴平面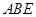 的法向量可取為
的法向量可取為 .
.
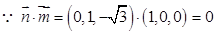 , ∴
, ∴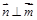 ,∴平面
,∴平面 平面
平面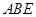 .
6分
.
6分
(Ⅱ)設平面 的法向量為
的法向量為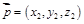 ,
,
則由
及
可取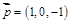
∵平面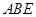 的法向量可取為
的法向量可取為 ,
,
∴銳二面角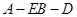 的余弦值為
的余弦值為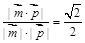 ,
,
∴二面角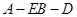 的大小為
的大小為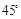 .
12分.
.
12分.
考點:空間位置關系、二面角、平面向量.


科目:高中數學 來源: 題型:
 18、如圖,在四棱錐P-ABCD中,側面PAD是正三角形,且與底面ABCD垂直,底面ABCD是邊長為2的菱形,∠BAD=60°,N是PB中點,過A、N、D三點的平面交PC于M.
18、如圖,在四棱錐P-ABCD中,側面PAD是正三角形,且與底面ABCD垂直,底面ABCD是邊長為2的菱形,∠BAD=60°,N是PB中點,過A、N、D三點的平面交PC于M.查看答案和解析>>
科目:高中數學 來源: 題型:
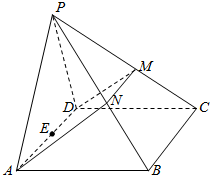 如圖,在四棱錐P-ABCD中,側面PAD是正三角形,且與底面ABCD垂直,底面ABCD是邊長為4的菱形,且∠BAD=60°,N是PB的中點,過A,D,N的平面交PC于M,E是AD的中點.
如圖,在四棱錐P-ABCD中,側面PAD是正三角形,且與底面ABCD垂直,底面ABCD是邊長為4的菱形,且∠BAD=60°,N是PB的中點,過A,D,N的平面交PC于M,E是AD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在四棱錐
如圖,在四棱錐![]() 中,側面
中,側面![]()
是正三角形,且與底面![]() 垂直,底面
垂直,底面![]() 是邊長為2的菱形,
是邊長為2的菱形,![]() ,
,![]() 是
是![]() 中點,過
中點,過![]() 、
、![]() 、
、![]() 三點的平面交
三點的平面交![]() 于
于![]() .
.
(1)求證:![]() ; (2)求證:
; (2)求證:![]() 是
是![]() 中點;(3)求證:平面
中點;(3)求證:平面![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)
如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() ,
,![]() 為
為![]() 的中點。
的中點。![]()
(1)點![]() 在線段
在線段![]() 上,
上,![]() ,
,
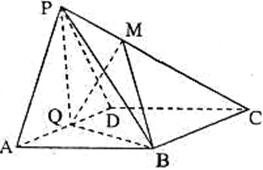 試確定
試確定![]() 的值,使
的值,使![]() 平面
平面![]() ;
;
(2)在(1)的條件下,若平面![]() 平
平
面ABCD,求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)
如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() ,
,![]() 為
為![]() 的中點。
的中點。

![]()
(1)點![]() 在線段
在線段![]() 上,
上,![]() ,
,
試確定![]() 的值,使
的值,使![]() 平面
平面![]() ;
;
(2)在(1)的條件下,若平面![]() 平
平
面ABCD,求二面角![]() 的大小。
的大小。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com