記定義在[-1,1]上的函數f(x)=x2+px+q(p,q∈R)的最大值與最小值分別為M,m.又記h(p)=M-m.
(Ⅰ)當0≤p≤2時,求M、m(用p,q表示),并證明h(p)≥1;
(Ⅱ)寫出h(p)的解析式(不必寫出求解過程);
(Ⅲ)在所有形如題設的函數f(x)中,求出這樣的f(x),使得|f(x)|的最大值為最小.
【答案】
分析:(Ⅰ)根據每件
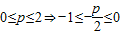
,又f(x)圖象開口向上,得出最大值與最小值,從而求得h(p)并證明h(p)≥1;
(Ⅱ)對字母p進行分類討論后寫出出h(p)的解析式即可;
(Ⅲ)由(Ⅱ)知h(p)的解析式,結合M-m≥1及取得最值的條件得出,p=0,M=1+q,m=q.最后結合由M=-m得1+q=-q求得q,最后寫出所求函數式即可.
解答:解:(Ⅰ)
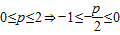
,又f(x)圖象開口向上,
∴
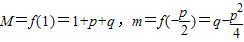
∴
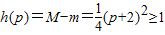
(4分)
(Ⅱ)
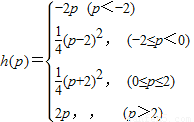
(Ⅲ)由(Ⅱ)知

,∴M-m≥1.
∵在[-1,1]上,總有
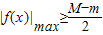
,當且僅當M=-m時取”=”;
又,
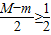
,當且僅當p=0時取“=”,
∴當
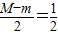
時的f(x)符合條件.
此時,p=0,M=1+q,m=q.由M=-m得1+q=-q.∴
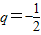
即所求函數為:f(x)=
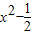
.(13分)
點評:本小題主要考查函數解析式的求解及常用方法、函數的最值及其幾何意義等基礎知識,考查運算求解能力與轉化思想.屬于基礎題.

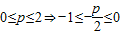 ,又f(x)圖象開口向上,得出最大值與最小值,從而求得h(p)并證明h(p)≥1;
,又f(x)圖象開口向上,得出最大值與最小值,從而求得h(p)并證明h(p)≥1;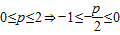 ,又f(x)圖象開口向上,
,又f(x)圖象開口向上,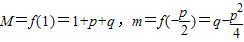
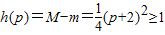 (4分)
(4分)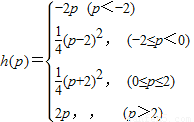
 ,∴M-m≥1.
,∴M-m≥1.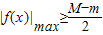 ,當且僅當M=-m時取”=”;
,當且僅當M=-m時取”=”;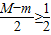 ,當且僅當p=0時取“=”,
,當且僅當p=0時取“=”,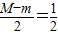 時的f(x)符合條件.
時的f(x)符合條件.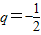
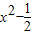 .(13分)
.(13分)
