變量x、y滿足
(1)設z＝
，求z的最小值；
(2)設z＝x2＋y2，求z的取值范圍．
（1）
；（2）
.
解析試題分析： 由題意畫出可行域，分別求出可行域各頂點
、
、
坐標.（1）將所求目標函數
構造為
，此時
可以看作是可行域內的點與原點連成直線的斜率的最小值，由于可行域范圍在第一象限內，所以可行域內的點與原點連線中傾斜角最小的為
，故
，再由頂點坐標可求出的最小值；（2）將目標函數
構造為
，此時可以看作是可行域內的點與原點之間距離的范圍，經查驗比較可得
，
，通過計算
、
的值可以求出所求的取值范圍.提示：在解決此類線性規劃問題中，常常把目標函數構造出斜截式的直線方程
、過原點直線的斜率
、與某一定點間的距離
等等，再通過求截距、斜率、距離來求出目標函數的值.
試題解析：由約束條件
，作出
可行域如圖所示.
3分
由
，解得
由
，解得
由
，解得
. 6分
（1）因為
，所以的值即是可行域中的點與原點
連線的斜率.
觀察圖形可知
9分
（2）的幾何意義是可行域上的點到原點的距離的平方，
結合圖形可知，可行域上的點到原點的距離中，
，
，
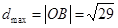所以所求的取值范圍為.
考點：1線性規劃問題；2.斜率的計算.
閱讀快車系列答案科目：高中數學 來源： 題型：解答題
某工廠有A、B兩種配件生產甲、乙兩種產品，每生產一種甲產品使用4個A配件耗時1h，每生產一件乙產品使用4個B配件耗時2h，該廠每天最多可從配件廠獲得16個A配件和12個B配件，按每天8h計算，若生產一件甲產品獲利2萬元，生產一件乙產品獲利3萬元，采用哪種生產安排利潤最大？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
假設每天從甲地去乙地的旅客人數X是服從正態分布N(800,502)的隨機變量．記一天中從甲地去乙地的旅客人數不超過900的概率為p0.
(1)求p0的值；(參考數據：若X～N(μ，σ2)，有P(μ－σ＜X≤μ＋σ)＝0.682 6，P(μ－2σ＜X≤μ＋2σ)＝0.954 4，P(μ－3σ＜X≤μ＋3σ)＝0.997 4)
(2)某客運公司用A、B兩種型號的車輛承擔甲、乙兩地間的長途客運業務，每車每天往返一次．A、B兩種車輛的載客量分別為36人和60人，從甲地去乙地的營運成本分別為1 600元/輛和2 400元/輛．公司擬組建一個不超過21輛車的客運車隊，并要求B型車不多于A型車7輛．若每天要以不小于p0的概率運完從甲地去乙地的旅客，且使公司從甲地去乙地的營運成本最小，那么應配備A型車、B型車各多少輛？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知x，y滿足約束條件
，試求解下列問題．
(1)z＝
的最大值和最小值；
(2)z＝
的最大值和最小值；
(3)z＝|3x＋4y＋3|的最大值和最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知關于
的二次函數
（1）設集合
和
分別從集合
和
中隨機取一個數作為
和
，求函數
在區間
上是增函數的概率.
（2）設點（a,b）是區域
內的隨機點，求函數
在區間上是增函數的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：單選題
要證a2+b2-1-a2b2≤0,只要證 ( )
| A．2ab-1-a2b2≤0 |
B．a2+b2-1- ≤0 |
C． -1-a2b2≤0 |
| D．(a2-1) (b2-1)≥0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
,
上的函數
滿足：
；
，且
，有
.
，則k的最小值為（ ）
滿足約束條件
，則目標函數
的最大值為 .