
定義在(-∞,0)∪(0,+∞)上的函數f(x),如果對于任意給定的等比數列{an},{f(an)}仍是等比數列,則稱f(x)為“保等比數列函數”。現有定義在( )
(-∞,0)∪(0,+∞)上的如下函數:①f(x)=x²;②f(x)=2x;③ ;④f(x)="ln|x" |。則其中是“保等比數列函數”的f(x)的序號為 ( )
;④f(x)="ln|x" |。則其中是“保等比數列函數”的f(x)的序號為 ( )
| A.①② | B.①③ | C.③④ | D.②④ |
科目:高中數學 來源: 題型:單選題
在函數y=f(x)的圖象上有點列(xn,yn),若數列{xn}是等差數列,數列{yn}是等比數列,則函數y=f(x)的解析式可能為( )
| A.f(x)=2x+1 | B.f(x)=4x2 |
| C.f(x)=log3x | D.f(x)= x x |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
1202年,意大利數學家斐波那契在他的書中給出了一個關于兔子繁殖的遞推關系: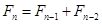 (
( ),其中
),其中 表示第
表示第 個月的兔子的總對數,
個月的兔子的總對數, ,則
,則 的值為( )
的值為( )
| A.13 | B.21 | C.34 | D.55 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com