已知函數f(x)=ax3+bx2的圖象在點(-1,2)處的切線恰好與x-3y=0垂直,又f(x)在[m,m+1]上單調遞增,則m的取值范圍是( )
A.(-∞,-3]
B.[0,+∞)
C.(-∞,-3)∪(0,+∞)
D.(-∞,-3]∪[0,+∞)
【答案】
分析:先求導函數,然后根據函數在點(-1,2)處的切線恰好與x-3y=0垂直建立方程組,解之即可得到函數f(x)的解析式,根據f(x)在[m,m+1]上單調遞增,則f′(x)≥0的解集包含區間[m,m+1],建立不等關系,解之即可.
解答:解:f′(x)=3ax
2+2bx,因為函數在點(-1,2)處的切線恰好與x-3y=0垂直得到切線的斜率為-3,
得到:
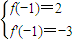
即
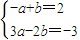
解得:
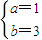
,則f(x)=x
3+3x
2f′(x)=3x
2+6x=3x(x+2)≥0解得:x≥0或x≤-2,即x≥0或x≤-2時,f(x)為增函數;
所以[m,m+1]?(-∞,-2]或[m,m+1]?[0,+∞)即m+1≤-2或m≥0,
解得m≤-3或m≥0
故選D.
點評:本題主要考查了利用導數研究曲線上某點切線方程,以及利用導數研究函數的單調性,同時考查了分析問題解決問題的能力,屬于中檔題.

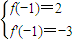 即
即 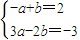
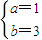 ,則f(x)=x3+3x2
,則f(x)=x3+3x2

 小學課時特訓系列答案
小學課時特訓系列答案