
(本小題15分)已知函數f(x)=(1+x)2-aln(1+x)2在(-2,-1)上是增函數,
在(-∞,-2)上為減函數.
(1)求f(x)的表達式;
(2)若當x∈ 時,不等式f(x)<m恒成立,求實數m的值;
時,不等式f(x)<m恒成立,求實數m的值;
(3)是否存在實數b使得關于x的方程f(x)=x2+x+b在區間[0,2]上恰好有兩個相異的實根,若存在,求實數b的取值范圍.
(1)f(x)=(1+x)2-ln(1+x)2.(2)需m>e2-2;
(3)存在這樣的實數b,當2-2ln2<b≤3-2ln3時滿足條件.
【解析】本試題主要是考查了函數單調性與導數的關系和函數奇偶性以及函數與不等式的關系的綜合運用。
(1)求解函數的導數 f′(x)=2(1+x)-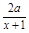
=2· ,
,
那么依題意f(x)在(-2,-1)上是增函數,在(-∞,-2)上為減函數.∴x=-2時,f(x)有極小值,∴f′(-2)=0.從而得到解析式。
(2)由于f′(x)=2(1+x)-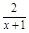 =
= ,易證函數在
,易證函數在 上單調遞減,
上單調遞減,
因此若使原不等式恒成立只需求解其最大值m>e2-2即可.
(3)若存在實數b使得條件成立,
方程f(x)=x2+x+b即為x-b+1-ln(1+x)2=0,
要使方程f(x)=x2+x+b在區間[0,2]上恰好有兩個相異的實根,只需g(x)=0在區間[0,1]和[1,2]上各有一個實根,于是有
 2-2ln2<b≤3-2ln3,
2-2ln2<b≤3-2ln3,
故存在這樣的實數b,當2-2ln2<b≤3-2ln3時滿足條件.
解 (1)∵f′(x)=2(1+x)-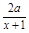
=2· ,
,
依題意f(x)在(-2,-1)上是增函數,在(-∞,-2)上為減函數.∴x=-2時,f(x)有極小值,∴f′(-2)=0.
代入方程解得a=1,
故f(x)=(1+x)2-ln(1+x)2.
(2)由于f′(x)=2(1+x)-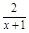 =
= ,
,
令f′(x)=0,得x1=0,x2=-2.
(由于x∈ ,故x2=-2舍去),
,故x2=-2舍去),
易證函數在 上單調遞減,
上單調遞減,
在[0,e-1]上單調遞增,
且f( )=
)=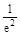 +2,f(e-1)=e2-2>
+2,f(e-1)=e2-2>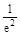 +2,
+2,
故當x∈ 時,f(x)max=e2-2,
時,f(x)max=e2-2,
因此若使原不等式恒成立只需m>e2-2即可.
(3)若存在實數b使得條件成立,
方程f(x)=x2+x+b
即為x-b+1-ln(1+x)2=0,
令g(x)=x-b+1-ln(1+x)2,
則g′(x)=1-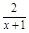 =
= ,
,
令g′(x)>0,得x<-1或x>1,
令g′(x)<0,得-1<x<1,
故g(x)在[0,1]上單調遞減,在[1,2]上單調遞增,要使方程f(x)=x2+x+b在區間[0,2]上恰好有兩個相異的實根,只需g(x)=0在區間[0,1]和[1,2]上各有一個實根,于是有
 2-2ln2<b≤3-2ln3,
2-2ln2<b≤3-2ln3,
故存在這樣的實數b,當2-2ln2<b≤3-2ln3時滿足條件.


科目:高中數學 來源:寧波市2010屆高三三模考試文科數學試題 題型:解答題
(本小題15分)已知函數 (
(
(1)若函數 在
在 處有極值為
處有極值為 ,求
,求 的值;
的值;
(2)若對任意 ,
, 在
在 上單調遞增,求
上單調遞增,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:全國高中數學聯合競賽一試 題型:解答題
(本小題15分)已知 ,
, 是實數,方程
是實數,方程 有兩個實根
有兩個實根 ,
, ,數列
,數列 滿足
滿足 ,
, ,
,
(Ⅰ)求數列 的通項公式(用
的通項公式(用 ,
, 表示);
表示);
(Ⅱ)若 ,
, ,求
,求 的前
的前 項和.
項和.
查看答案和解析>>
科目:高中數學 來源:寧波市2010屆高三三模考試文科數學試題 題型:解答題
(本小題15分)已知拋物線 ,過點
,過點 的直線
的直線 交拋物線
交拋物線 于
于 兩點,且
兩點,且 .
.
(1)求拋物線 的方程;
的方程;
(2)過點 作
作 軸的平行線與直線
軸的平行線與直線 相交于點
相交于點 ,若
,若 是等腰三角形,求直線
是等腰三角形,求直線 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com