
【題目】2018以來,依托用戶碎片化時間的娛樂需求、分享需求以及視頻態的信息負載力,短視頻快速崛起;與此同時,移動閱讀方興未艾,從側面反應了人們對精神富足的一種追求,在習慣了大眾娛樂所帶來的短暫愉悅后,部分用戶依舊對有著傳統文學底蘊的嚴肅閱讀青睞有加.某讀書APP抽樣調查了非一線城市![]() 和一線城市
和一線城市![]() 各100名用戶的日使用時長(單位:分鐘),繪制成頻率分布直方圖如下,其中日使用時長不低于60分鐘的用戶記為“活躍用戶”.
各100名用戶的日使用時長(單位:分鐘),繪制成頻率分布直方圖如下,其中日使用時長不低于60分鐘的用戶記為“活躍用戶”.
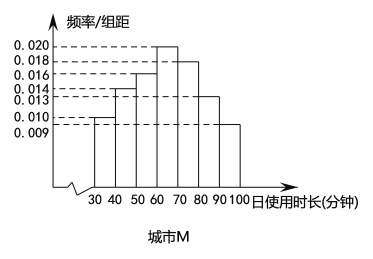
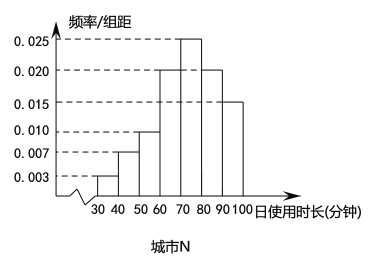
(1)請填寫以下![]() 列聯表,并判斷是否有99%的把握認為用戶活躍與否與所在城市有關?
列聯表,并判斷是否有99%的把握認為用戶活躍與否與所在城市有關?
活躍用戶 | 不活躍用戶 | 合計 | |
城市 | |||
城市 | |||
合計 |
臨界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
參考公式: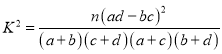 .
.
(2)以頻率估計概率,從城市![]() 中任選2名用戶,從城市
中任選2名用戶,從城市![]() 中任選1名用戶,設這3名用戶中活躍用戶的人數為
中任選1名用戶,設這3名用戶中活躍用戶的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
【答案】(1)填表見解析;有99%的把握認為用戶是否活躍與所在城市有關;(2)分布列見解析;期望為2.
【解析】
(1)根據頻率分布直方圖分別求出城市![]() 、
、![]() 中的活躍用戶與不活躍用戶,即可得出列聯表.
中的活躍用戶與不活躍用戶,即可得出列聯表.
(2)由統計數據可知,城市![]() 中活躍用戶占
中活躍用戶占![]() ,城市N中活躍用戶占
,城市N中活躍用戶占![]() ,設從
,設從![]() 城市中任選的2名用戶中活躍用戶數為
城市中任選的2名用戶中活躍用戶數為![]() ,
,![]() ,設從
,設從![]() 城市中任選的1名用戶中活躍用戶數為
城市中任選的1名用戶中活躍用戶數為![]() ,
,![]() 服從兩點分布,
服從兩點分布,![]() ,利用二項分布求出概率即可得出分布列,再利用期望公式即可求解.
,利用二項分布求出概率即可得出分布列,再利用期望公式即可求解.
由已知可得以下![]() 列聯表:
列聯表:
活躍用戶 | 不活躍用戶 | 合計 | |
城市 | 60 | 40 | 100 |
城市 | 80 | 20 | 100 |
合計 | 140 | 60 | 200 |
計算![]() ,
,
所以有99%的把握認為用戶是否活躍與所在城市有關.
(2)由統計數據可知,城市![]() 中活躍用戶占
中活躍用戶占![]() ,城市N中活躍用戶占
,城市N中活躍用戶占![]() ,
,
設從![]() 城市中任選的2名用戶中活躍用戶數為
城市中任選的2名用戶中活躍用戶數為![]() ,則
,則![]()
設從![]() 城市中任選的1名用戶中活躍用戶數為
城市中任選的1名用戶中活躍用戶數為![]() ,則
,則![]() 服從兩點分布,
服從兩點分布,
其中![]() .故
.故![]() ,
,
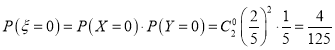 ;
;
![]()
![]() ;
;
![]()
![]() ;
;
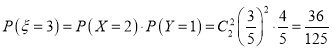 .
.
故所求![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD的底面ABCD為正方形,![]() ,E,F分別是棱PC,AB的中點.
,E,F分別是棱PC,AB的中點.
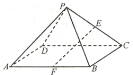
(1)求證:![]() 平面PAD;
平面PAD;
(2)若![]() ,求直線EF與平面PAB所成角的正弦值.
,求直線EF與平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .將曲線
.將曲線![]() 上每一點的橫坐標伸長到原來的兩倍(縱坐標不變)得到曲線
上每一點的橫坐標伸長到原來的兩倍(縱坐標不變)得到曲線![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】考慮![]() 的方格表,其中每個方格內均填有數字0.每次操作可先選定三個實數
的方格表,其中每個方格內均填有數字0.每次操作可先選定三個實數![]() 、
、![]() 、
、![]() ,然后選定一行,將這一行每個方格中的數都加上
,然后選定一行,將這一行每個方格中的數都加上![]() (
(![]() 為該方格所在的列數,
為該方格所在的列數,![]() );或選定一列,將這一列每個方格中的數都加上
);或選定一列,將這一列每個方格中的數都加上![]() (
(![]() 為該方格所在的行數,
為該方格所在的行數,![]() ),問:能否經過有限次操作,使該方格表中四個角的數字變成1,而其他格的數字仍為0?
),問:能否經過有限次操作,使該方格表中四個角的數字變成1,而其他格的數字仍為0?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將![]() 方格表的每個方格任意填入
方格表的每個方格任意填入![]() 或
或![]() ,然后允許進行如下操作:每次任意選擇一行(或列),將這一行(或列)中的數全部變號.若無論開始時方格表的數怎樣填,總能經過不超過
,然后允許進行如下操作:每次任意選擇一行(或列),將這一行(或列)中的數全部變號.若無論開始時方格表的數怎樣填,總能經過不超過![]() 次操作,使得方格表每一行中所有數的和、每一列中所有數的和均非負.試確定
次操作,使得方格表每一行中所有數的和、每一列中所有數的和均非負.試確定![]() 的最小值
的最小值![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年12月18日上午10時,在人民大會堂舉行了慶祝改革開放40周年大會.40年眾志成城,40年砥礪奮進,40年春風化雨,中國人民用雙手書寫了國家和民族發展的壯麗史詩.會后,央視媒體平臺,收到了來自全國各地的紀念改革開放40年變化的老照片,并從眾多照片中抽取了100張照片參加“改革開放40年圖片展”,其作者年齡集中在![]() 之間,根據統計結果,做出頻率分布直方圖如下:
之間,根據統計結果,做出頻率分布直方圖如下:

(Ⅰ)求這100位作者年齡的樣本平均數![]() 和樣本方差
和樣本方差![]() (同一組數據用該區間的中點值作代表);
(同一組數據用該區間的中點值作代表);
(Ⅱ)由頻率分布直方圖可以認為,作者年齡X服從正態分布![]() ,其中
,其中![]() 近似為樣本平
近似為樣本平
均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .
.
(i)利用該正態分布,求![]() ;
;
(ii)央視媒體平臺從年齡在![]() 和
和![]() 的作者中,按照分層抽樣的方法,抽出了7人參加“紀念改革開放40年圖片展”表彰大會,現要從中選出3人作為代表發言,設這3位發言者的年齡落在區間
的作者中,按照分層抽樣的方法,抽出了7人參加“紀念改革開放40年圖片展”表彰大會,現要從中選出3人作為代表發言,設這3位發言者的年齡落在區間![]() 的人數是Y,求變量Y的分布列和數學期望.附:
的人數是Y,求變量Y的分布列和數學期望.附:![]() ,若
,若![]() ,則
,則![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2022年北京冬奧運動會即第24屆冬季奧林匹克運動會將在2022年2月4日至2月20日在北京和張家口舉行,某研究機構為了了解大學生對冰壺運動的興趣,隨機從某大學生中抽取了120人進行調查,經統計男生與女生的人數比為11:13,男生中有30人表示對冰壺運動有興趣,女生中有15人對冰壺運動沒有興趣.
(1)完成![]() 列聯表,并判斷能否有99%的把握認為“對冰壺運動是否有興趣與性別有關”?
列聯表,并判斷能否有99%的把握認為“對冰壺運動是否有興趣與性別有關”?
有興趣 | 沒有興趣 | 合計 | |
男 | 30 | ||
女 | 15 | ||
合計 | 120 |
(2)用分層抽樣的方法從樣本中對冰壺運動有興趣的學生中抽取8人,求抽取的男生和女生分別為多少人?若從這8人中選取兩人作為冰壺運動的宣傳員,求選取的2人中恰好有1位男生和1位女生的概率.
附:![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com