
【題目】如圖所示,在多面體![]() 中,四邊形
中,四邊形![]() 與四邊形
與四邊形![]() 均為邊長為2的正方形,
均為邊長為2的正方形,![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
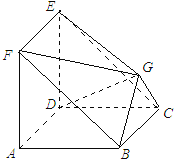
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求多面體![]() 的體積.
的體積.
【答案】見解析
【解析】(1)∵平面![]() 平面
平面![]() ,且
,且![]() ,∴
,∴![]() 平面
平面![]() .……………1分
.……………1分
∵![]() 平面
平面![]() ,∴
,∴![]() .……………2分
.……………2分
又∵![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .……………4分
.……………4分
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .……………5分
.……………5分
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,則
,則
![]() .……………6分
.……………6分
∵平面![]() 平面
平面![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 為四棱錐
為四棱錐![]() 的高,且
的高,且![]() .……………7分
.……………7分
又∵![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴點![]() 到平面
到平面![]() 的距離就是點
的距離就是點![]() 到平面
到平面![]() 的距離,即為2,
的距離,即為2,
點![]() 到平面
到平面![]() 的距離就是點
的距離就是點![]() 到平面
到平面![]() 的距離,即為1.……………9分
的距離,即為1.……………9分
同理,點![]() 到平面
到平面![]() 的距離就是點
的距離就是點![]() 到平面
到平面![]() 的距離,即為1,……………10分
的距離,即為1,……………10分
∴![]()
![]() .……………12分
.……………12分
(或計算![]() )
)
【命題意圖】本題主要考查空間平面與平面的垂直關系、四棱錐的體積,意在考查邏輯思維能力、空間想
象能力、邏輯推理論證能力、計算能力.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在直角梯形ABCD中AD∥BC,∠ADC=90°,平面ABCD外一點P在平面ABCD內的射影Q恰在邊AD上, PA=AD=2 BC=2,CD=.
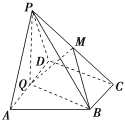
(1)若平面PQB⊥平面PAD,求證:Q為線段AD中點;
(2)在(1)的條件下,若M在線段PC上,且PA∥平面BMQ,求點M到平面PAB的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市文化部門為了了解本市市民對當地地方戲曲是否喜愛,從15-65歲的人群中隨機抽樣了![]() 人,得到如下的統計表和頻率分布直方圖.
人,得到如下的統計表和頻率分布直方圖.
(1)寫出其中的![]() 、
、![]() 、
、![]() 及
及![]() 和
和![]() 的值;
的值;
(2)若從第1,2,3組回答喜歡地方戲曲的人中用分層抽樣的方法抽取6人,求這三組每組分別抽取多少人?
(3)在(2)抽取的6人中隨機抽取2人,求這2人都是第3組的概率

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集U=R,集合A={x|﹣1≤x<3},B={x|2x﹣4≥x﹣2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},滿足B∪C=C,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個質地均勻的正四面體的四個面上分別標示著數字1,2,3,4,一個質地均勻的骰子(正方體)的六個面上分別標示數字1,2,3,4,5,6,先后拋擲一次正四面體和骰子.
(1)列舉出全部基本事件;
(2)求被壓在底部的兩個數字之和小于5的概率;
(3)求正四面體上被壓住的數字不小于骰子上被壓住的數字的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com