
【題目】已知函數![]() ,
,![]() ,
,![]() .
.
(1)若函數![]() 在
在![]() 上是單調函數,求實數m的取值范圍;
上是單調函數,求實數m的取值范圍;
(2)當![]() 時,
時,
(i)求函數![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(ii)若對任意![]() ,不等式
,不等式![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
【答案】(1)![]()
(2)(i)![]() ,(ii)
,(ii)![]()
【解析】
(Ⅰ)求出原函數的導函數,利用導函數恒大于等于0或恒小于等于0求解![]() 的取值范圍;
的取值范圍;
(Ⅱ)當![]() 時,
時,![]()
![]() ,
,![]()
![]() ,
,
![]() 求得
求得![]() 與
與![]() ,再由直線方程的點斜式求解;
,再由直線方程的點斜式求解;
![]() 證明當
證明當![]() ,
,![]() 時,
時,![]() ,
,![]() ,可得
,可得![]() 時不等式
時不等式![]() 恒成立,然后利用導數證明
恒成立,然后利用導數證明![]() 時不等式不成立,則答案可求.
時不等式不成立,則答案可求.
解:(1)![]() ,
,
因為函數![]() 在
在![]() 上是單調函數,
上是單調函數,
所以函數![]() 在
在![]() 上是單調遞增函數或是單調遞減函數,
上是單調遞增函數或是單調遞減函數,
即![]() 或
或![]() 恒成立,也即
恒成立,也即![]() 或
或![]() 在
在![]() 上恒成立.
上恒成立.
當![]() 時,
時,![]() ,
,
所以![]() .
.
(2)當![]() 時,
時,![]() ,
,![]() .
.
(i)因為![]() ,所以
,所以![]() .
.
又![]() ,所以函數
,所以函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(ii)由(i)知函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,
,
下面先證明![]() ,
,![]() .
.
證明:設函數![]() ,
,![]() ,
,
![]() .
.
因為![]() ,所以
,所以![]() ,
,
所以函數![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() ,所以
,所以![]() .
.
所以![]() ,
,![]() .①
.①
接下來證明:當![]() 時,
時,![]() .
.
設函數![]() ,則
,則![]() ,
,
所以當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞減.
上單調遞減.
又![]() ,所以
,所以![]() ,故
,故![]() ,
,![]() .②
.②
依據①②式可知,當![]() 時,
時,![]() 顯然成立.
顯然成立.
當![]() 時,設
時,設![]() ,
,
則![]() ,
,
取![]() ,
,![]() ,
,
則 .
.
又因為![]() ,由零點存在性判定方法可知:必存在
,由零點存在性判定方法可知:必存在![]() ,使得
,使得![]() .
.
當![]() 時,
時,![]() ,此時
,此時![]() 單調遞減,又
單調遞減,又![]() ,所以
,所以![]() ,矛盾.
,矛盾.
綜上可知:![]() .
.


 應用題作業本系列答案
應用題作業本系列答案科目:高中數學 來源: 題型:
【題目】某市政府為了引導居民合理用水,決定全面實施階梯水價,居民用水原則上以住宅為單位(一套住宅為一戶).
階梯級別 | 第一階梯 | 第二階梯 | 第三階梯 |
月用水范圍(噸) |
|
|
|
為了了解全市居民月用水量的分布情況,通過抽樣,獲得了![]() 戶居民的月用水量(單位:噸),得到統計表如下:
戶居民的月用水量(單位:噸),得到統計表如下:
居民用水戶編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用水量(噸) | 7 | 8 | 8 | 9 | 10 | 11 | <>13 | 14 | 15 | 20 |
(1)若用水量不超過![]() 噸時,按
噸時,按![]() 元/噸計算水費;若用水量超過
元/噸計算水費;若用水量超過![]() 噸且不超過
噸且不超過![]() 噸時,超過
噸時,超過![]() 噸部分按
噸部分按![]() 元/噸計算水費;若用水量超過
元/噸計算水費;若用水量超過![]() 噸時,超過
噸時,超過![]() 噸部分按
噸部分按![]() 元/噸計算水費.試計算:若某居民用水
元/噸計算水費.試計算:若某居民用水![]() 噸,則應交水費多少元?
噸,則應交水費多少元?
(2)現要在這![]() 戶家庭中任意選取
戶家庭中任意選取![]() 戶,求取到第二階梯水量的戶數的分布列與期望;
戶,求取到第二階梯水量的戶數的分布列與期望;
(3)用抽到的![]() 戶家庭作為樣本估計全市的居民用水情況,從全市依次隨機抽取
戶家庭作為樣本估計全市的居民用水情況,從全市依次隨機抽取![]() 戶,若抽到
戶,若抽到![]() 戶月用水量為第一階梯的可能性最大,求
戶月用水量為第一階梯的可能性最大,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數 ,下列判斷正確的是( )
,下列判斷正確的是( )
A. ![]() 有最大值和最小值
有最大值和最小值
B. ![]() 的圖象的對稱中心為
的圖象的對稱中心為![]() (
(![]() )
)
C. ![]() 在
在![]() 上存在單調遞減區間
上存在單調遞減區間
D. ![]() 的圖象可由
的圖象可由![]() 的圖象向左平移
的圖象向左平移![]() 個單位而得
個單位而得
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由于當前學生課業負擔較重,造成青少年視力普遍下降,現從湖口中學隨機抽取16名學生,經校醫用視力表檢查得到每個學生的視力狀況的莖葉圖(以小數點前的一位數字為莖,小數點后的一位數字為葉)如下:

(1)指出這組數據的眾數和中位數;
(2)若視力測試結果不低于5.0則稱為“好視力”,求校醫從這16人中選取3人,至多有1人是“好視力”的概率;
(3)以這16人的樣本數據來估計整個學校的總體數據,若從該校(人數很多)任選3人,記![]() 表示抽到“好視力”學生的人數,求
表示抽到“好視力”學生的人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求函數
,求函數 在
在![]() 處的切線方程;
處的切線方程;
(2)若![]() ,且
,且![]() 是函數
是函數![]() 的一個極值點,確定
的一個極值點,確定![]() 的單調區間;
的單調區間;
(3)若![]() ,
,![]() 且對任意
且對任意![]() ,
, 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 在圓
在圓![]() :
:![]() 上運動,點
上運動,點![]() 在
在![]() 軸上的投影為
軸上的投影為![]() ,動點
,動點![]() 滿足
滿足![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的動直線
的動直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,問:在
兩點,問:在![]() 軸上是否存在定點
軸上是否存在定點![]() 使得
使得![]() 的值為定值?若存在,求出定點
的值為定值?若存在,求出定點![]() 的坐標及該定值;若不存在,請說明理由.
的坐標及該定值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知鮮切花![]() 的質量等級按照花枝長度
的質量等級按照花枝長度![]() 進行劃分,劃分標準如下表所示.
進行劃分,劃分標準如下表所示.
花枝長度 |
|
|
|
鮮花等級 | 三級 | 二級 | 一級 |
某鮮切花加工企業分別從甲乙兩個種植基地購進鮮切花![]() ,現從兩個種植基地購進的鮮切花
,現從兩個種植基地購進的鮮切花![]() 中分別隨機抽取30個樣品,測量花枝長度并進行等級評定,所抽取樣品數據如圖所示.
中分別隨機抽取30個樣品,測量花枝長度并進行等級評定,所抽取樣品數據如圖所示.
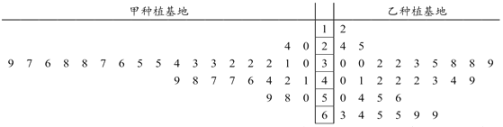
(1)根據莖葉圖比較兩個種植基地鮮切花![]() 的花枝長度的平均值及分散程度(不要求計算具體值,給出結論即可);
的花枝長度的平均值及分散程度(不要求計算具體值,給出結論即可);
(2)若從等級為三級的樣品中隨機選取2個進行新產品試加工,求選取的2個全部來自乙種植基地的概率;
(3)根據該加工企業的加工和銷售記錄,了解到來自乙種植基地的鮮切花![]() 的加工產品的單件利潤為4元;來自乙種植基地的鮮切花
的加工產品的單件利潤為4元;來自乙種植基地的鮮切花![]() 的加工產品的單件成本為10元,銷售率(某等級產品的銷量與產量的比值)及單價如下表所示.
的加工產品的單件成本為10元,銷售率(某等級產品的銷量與產量的比值)及單價如下表所示.
三級花加工產品 | 二級花加工產品 | 一級花加工產品 | |
銷售率 |
|
|
|
單價/(元/件) | 12 | 16 | 20 |
由于鮮切花![]() 加工產品的保鮮特點,未售出的產品均可按原售價的50%處理完畢.用樣本估計總體,如果僅從單件產品的利潤的角度考慮,該鮮切花加工企業應該從哪個種植基地購進鮮切花
加工產品的保鮮特點,未售出的產品均可按原售價的50%處理完畢.用樣本估計總體,如果僅從單件產品的利潤的角度考慮,該鮮切花加工企業應該從哪個種植基地購進鮮切花![]() ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年
年![]() 月
月![]() 日,國務院總理李克強在做政府工作報告時說,打好精準脫貧攻堅戰.江西省貧困縣脫貧摘帽取得突破性進展:
日,國務院總理李克強在做政府工作報告時說,打好精準脫貧攻堅戰.江西省貧困縣脫貧摘帽取得突破性進展:![]() 年,穩定實現扶貧對象“兩不愁、三保障”,貧困縣全部退出.圍繞這個目標,江西正著力加快增收步伐,提高救助水平,改善生活條件,打好產業扶貧、保障扶貧、安居扶貧三場攻堅戰.為響應國家政策,老張自力更生開了一間小型雜貨店.據長期統計分析,老張的雜貨店中某貨物每天的需求量
年,穩定實現扶貧對象“兩不愁、三保障”,貧困縣全部退出.圍繞這個目標,江西正著力加快增收步伐,提高救助水平,改善生活條件,打好產業扶貧、保障扶貧、安居扶貧三場攻堅戰.為響應國家政策,老張自力更生開了一間小型雜貨店.據長期統計分析,老張的雜貨店中某貨物每天的需求量![]() 在
在![]() 與
與![]() 之間,日需求量
之間,日需求量![]() (件)的頻率
(件)的頻率![]() 分布如下表所示:
分布如下表所示:
![]()
己知其成本為每件![]() 元,售價為每件
元,售價為每件![]() 元若供大于求,則每件需降價處理,處理價每件
元若供大于求,則每件需降價處理,處理價每件![]() 元.
元.
(1)設每天的進貨量為![]() ,視日需求量
,視日需求量![]() 的頻率為概率
的頻率為概率![]() ,求在每天進貨量為
,求在每天進貨量為![]() 的條件下,日銷售量
的條件下,日銷售量![]() 的期望值
的期望值![]() (用
(用![]() 表示);
表示);
(2)在(1)的條件下,寫出![]() 和
和![]() 的關系式,并判斷
的關系式,并判斷![]() 為何值時,日利潤的均值最大.
為何值時,日利潤的均值最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() ,若滿足:對任意
,若滿足:對任意![]() ,存在常數
,存在常數![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是
是![]() 上的有界函數,其中
上的有界函數,其中![]() 稱為函數
稱為函數![]() 的上界
的上界
(1)設![]() ,判斷
,判斷![]() 在
在![]() 上是否是有界函數,若是,說明理由,并寫出
上是否是有界函數,若是,說明理由,并寫出![]() 所有上界的值的集合;若不是,也請說明理由.
所有上界的值的集合;若不是,也請說明理由.
(2)若函數![]() 在
在![]() 上是以
上是以![]() 為上界的有界函數,求實數
為上界的有界函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com