【題目】已知偶函數
在
上單調遞增，則
A. 
B. 
C. 
D. 
【答案】D
【解析】分析：根據偶函數的定義，以及f（x）在（0，+∞）上單調遞增，這樣根據函數單調性定義以及冪函數、指數函數和對數函數的單調性即可判斷每個選項的正誤，從而選出正確選項．
詳解：f（x）為偶函數，且在（0，+∞）上單調遞增；
A．f（﹣3e）=f（3e），且2e＜3e；
∴f（2e）＜f（3e）；
∴f（2e）＜f（﹣3e），∴該選項錯誤；
B．f（﹣e3）=f（e3），且e2＜e3；
∴f（e2）＜f（e3）；
∴f（e2）＜f（﹣e3），∴該選項錯誤；
C.
，
；
∴
；
∵f（x）是偶函數，且在（0，+∞）上單調遞增；
∴f（x）在（﹣∞，0）上單調遞減；
∴
，∴該選項錯誤；
D.
，
；
∴
；
∴
，∴該選項正確．
故答案為：D
提分百分百檢測卷系列答案
寶貝計劃期末沖刺奪100分系列答案
能考試全能100分系列答案科目：高中數學 來源： 題型：
【題目】已知f（x）=2sin（2x+ 
），若將它的圖象向右平移 個單位，得到函數g（x）的圖象，則函數g（x）圖象的一條對稱軸的方程為（ ）
A.x= 
B.x= 
C.x= 
D.x= 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=xea﹣x+bx，曲線y=f（x）在點（2，f（2））處的切線方程為y=（e﹣1）x+4，
（1）求a，b的值；
（2）求f（x）的單調區間．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在如圖所示的幾何體中，四邊形ABCD為正方形，PA⊥平面ABCD，PA∥BE，AB=PA=4，BE=2．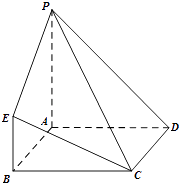 
（1）求證：CE∥平面PAD；
（2）求PD與平面PCE所成角的正弦值；
（3）在棱AB上是否存在一點F，使得平面DEF⊥平面PCE？如果存在，求 
的值；如果不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，圓C的方程為（x﹣ 
）2+（y+1）2=9，以O為極點，x軸的非負半軸為極軸建立極坐標系．
（1）求圓C的極坐標方程；
（2）直線OP：θ= 
（p∈R）與圓C交于點M，N，求線段MN的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國古代數學典籍《九章算術》“盈不足”中有一道兩鼠穿墻問題：“今有垣厚十尺，兩鼠對穿，初日各一尺，大鼠日自倍，小鼠日自半，問幾何日相逢？”現用程序框圖描述，如圖所示，則輸出結果n=（ ）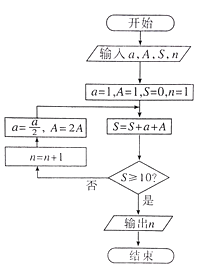 
A.4
B.5
C.2
D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓： 
（a＞b＞0），左右焦點分別是F1 ， F2 ， 焦距為2c，若直線 
與橢圓交于M點，滿足∠MF1F2=2∠MF2F1 ， 則離心率是（ ）
A.
B.
-1
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
(a>b>0)的一個頂點為A(2,0)，離心率為
.直線y＝k(x－1)與橢圓C交于不同的兩點M，N.
(1)求橢圓C的方程；
(2)當△AMN的面積為
時，求k的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）的定義域為R．a，b∈R，若此函數同時滿足：
①當a+b=0時，有f（a）+f（b）=0；
②當a+b＞0時，有f（a）+f（b）＞0，
則稱函數f（x）為Ω函數．
在下列函數中：
①y=x+sinx；
②y=3x﹣（ 
）x；
③y=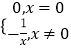 
是Ω函數的為 ． （填出所有符合要求的函數序號）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com