
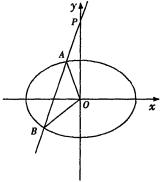
已知橢圓的中心在坐標原點O,焦點在x軸上,橢圓的短軸端點和焦點所組成的四邊形為正方形,兩準線間的距離為4.
(Ⅰ)求橢圓的方程;
(Ⅱ)直線l過點P(0,2)且與橢圓相交于A、B兩點,當ΔAOB面積取得最大值時,求直線l的方程.
設橢圓方程為![]() =1(a>b>0).
=1(a>b>0).
(Ⅰ)由已知得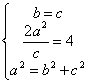
![]()
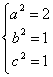 .
.
∴所求橢圓方程為![]() +y2=1.
+y2=1.
(Ⅱ)解法一:由題意知直線l的斜率存在,
設直線l的方程為y=kx+2,A(x1,y1),B(x2,y2),
由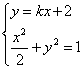 ,消去y得關于x的方程:
,消去y得關于x的方程:
(1+2k2)x2+8kx+6=0,
由直線l與橢圓相交于A、B兩點,∴△>0 ![]() 64k2-24(1+2k2)>0,
64k2-24(1+2k2)>0,
解得 k2>![]() ,
,
又由韋達定理得 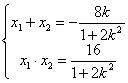
∴|AB|=![]() |x1-x2|=
|x1-x2|=![]()
![]()
=![]()
原點O到直線l的距離d=![]() .
.
∴S△AOB=![]() |AB|·d=
|AB|·d=![]() .
.
解法1:對S=![]() 兩邊平方整理得:
兩邊平方整理得:
4S2k4+4(S2-4)k2+S2+24=0 (*)
∵S≠0,
∴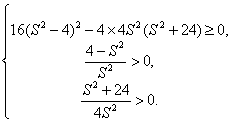
整理得:S2≤![]() .
.
又S>0,
∴0<S≤![]() .
.
從而S△AOB的最大值為S=![]() ,
,
此時代入方程(*)得
4k4-28k2+49=0
∴k=±![]()
所以,所求直線方程為:±![]() x-2y+4=0.
x-2y+4=0.
解法2:令m=![]() (m>0),
(m>0),
則2k2=m2+3.
∴S=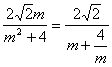 ≤
≤![]() .
.
當且僅當m=![]() 即m=2時,
即m=2時,
Smax=![]() .
.
此時k=±![]() .
.
所以,所求直線方程為±![]() x-2y+4=0.
x-2y+4=0.
解法二:由題意知直線l的斜率存在且不為零.
設直線l的方程為y=kx+2,A(x1,y1),B(x2,y2),
則直線l與x軸的交點D(-![]() ,0),
,0),
由解法一知 k2>![]() 且
且 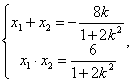
解法1:S△AOB=![]() |OD|·|y1-y2|=
|OD|·|y1-y2|=![]() |
|![]() |·|kx1+2-kx2-2|
|·|kx1+2-kx2-2|
=|x1-x2|
=![]()
=![]()
=![]() .
.
下同解法一.
解法2:S△AOB=S△POB-S△POA=![]() ×2×||x2|-|x1||=|x2-x1|=
×2×||x2|-|x1||=|x2-x1|=![]() .
.
下同解法一.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
| x2 |
| 4 |
| y2 |
| 9 |
| π |
| 2 |
| π |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
己知在銳角ΔABC中,角![]() 所對的邊分別為
所對的邊分別為![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)當![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.

20.如圖1,在平面內,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,將
是正三角形,將![]() 沿
沿![]() 折起,使
折起,使![]() 如圖2,
如圖2,![]() 為
為![]() 的中點,設直線
的中點,設直線![]() 過點
過點![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,點
所在平面,點![]() 是直線
是直線![]() 上的一個動點,且與點
上的一個動點,且與點![]() 位于平面
位于平面![]() 的同側。
的同側。
(1)求證:![]() 平面
平面![]() ;
;
(2)設二面角![]() 的平面角為
的平面角為![]() ,若
,若![]() ,求線段
,求線段![]() 長的取值范圍。
長的取值范圍。


21.已知A,B是橢圓![]() 的左,右頂點,
的左,右頂點,![]() ,過橢圓C的右焦點F的直線交橢圓于點M,N,交直線
,過橢圓C的右焦點F的直線交橢圓于點M,N,交直線![]() 于點P,且直線PA,PF,PB的斜率成等差數列,R和Q是橢圓上的兩動點,R和Q的橫坐標之和為2,RQ的中垂線交X軸于T點
于點P,且直線PA,PF,PB的斜率成等差數列,R和Q是橢圓上的兩動點,R和Q的橫坐標之和為2,RQ的中垂線交X軸于T點
(1)求橢圓C的方程;
 (2)求三角形MNT的面積的最大值
(2)求三角形MNT的面積的最大值
22. 已知函數![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值與最小值,且其最大值與最小值的和為
上存在最大值與最小值,且其最大值與最小值的和為![]() ,試求
,試求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 為奇函數:
為奇函數:
(1)是否存在實數![]() ,使得
,使得![]() 在
在![]() 為增函數,
為增函數,![]() 為減函數,若存在,求出
為減函數,若存在,求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(2)如果當![]() 時,都有
時,都有![]() 恒成立,試求
恒成立,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)
已知點![]() ,過點
,過點![]() 作拋物線
作拋物線![]()
![]() 的切線
的切線![]() ,切點
,切點![]() 在第二象限,如圖.
在第二象限,如圖.
 (Ⅰ)求切點
(Ⅰ)求切點![]() 的縱坐標;
的縱坐標;
(Ⅱ)若離心率為![]() 的橢圓
的橢圓![]() 恰好經過切點
恰好經過切點![]() ,設切線
,設切線![]() 交橢圓的另一點為
交橢圓的另一點為![]() ,記切線
,記切線![]() 的斜率分別為
的斜率分別為![]() ,若
,若![]() ,求橢圓方程.
,求橢圓方程.
21(本小題滿分12分)
已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)當![]() 時,
時,![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)證明:![]()
![]() .
.
22.選修4-1:幾何證明選講
如圖,![]() 是圓
是圓![]() 的直徑,
的直徑,![]() 是弦,
是弦,![]() 的平分線
的平分線![]() 交圓
交圓![]() 于點
于點![]() ,
,![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,
,![]() 交
交![]() 于點
于點![]() 。
。
 (1)求證:
(1)求證:![]() 是圓
是圓![]() 的切線;
的切線;
(2)若![]() ,求
,求![]() 的值。
的值。
23.選修4—4:坐標系與參數方程
在平面直角坐標系中,直線![]() 過點
過點![]() 且傾斜角為
且傾斜角為![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸的非負半軸為極軸,建立極坐標系,曲線
軸的非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點;
兩點;
(1)若![]() ,求直線
,求直線![]() 的傾斜角
的傾斜角![]() 的取值范圍;
的取值范圍;
(2)求弦![]() 最短時直線
最短時直線![]() 的參數方程。
的參數方程。
24. 選修4-5 不等式選講
已知函數![]()
(I)試求![]() 的值域;
的值域;
(II)設![]() ,若對
,若對![]() ,恒有
,恒有![]() 成立,試求實數a的取值范圍。
成立,試求實數a的取值范圍。
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省南通市海門中學高三(上)開學檢測數學試卷(解析版) 題型:解答題
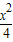 +
+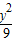 =1在M-1的作用下的新曲線的方程.
=1在M-1的作用下的新曲線的方程. ),若直線l過點P,且傾斜角為
),若直線l過點P,且傾斜角為 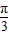 ,圓C以M為圓心、4為半徑.
,圓C以M為圓心、4為半徑.查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省南通市海門中學高三(上)開學檢測數學試卷(解析版) 題型:解答題
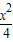 +
+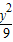 =1在M-1的作用下的新曲線的方程.
=1在M-1的作用下的新曲線的方程.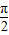 ),若直線l過點P,且傾斜角為
),若直線l過點P,且傾斜角為 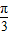 ,圓C以M為圓心、4為半徑.
,圓C以M為圓心、4為半徑.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com