Question

【題目】已知函數（）.

（1）求函數的單調區間；

（2）試問：函數圖像上是否存在不同兩點，使得在處的切線平行于直線，若存在，求出的坐標，若不存在，說明理由.

Answer 1

【答案】（1）在上單調遞增，在上單調遞減；（2）證明見解析.

【解析】試題分析：

（1）結合函數的解析式可得，據此可得在上單調遞增，在上單調遞減.

（2）假設存在兩點，不妨設，則，且函數在處的切線斜率，據此整理計算有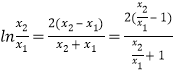： ，令，則，則：，，利用導函數研究函數的性質可得在內不存在，使得 ，則函數圖象上是不存在滿足題意的點.

試題解析：

（1）由，又 得

故，當時，，當時，

在上單調遞增，在上單調遞減；

（2）假設存在兩點，不妨設，則：

，

，

故=，

在函數圖象處的切線斜率，

得： ，

化簡得：， ，

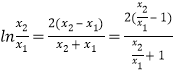令，則，上式化為：，即，

若令，，

由， 在上單調遞增，，

這表明在內不存在，使得 .

綜上，函數圖象上是不存在不同兩點，使得 在處的切線平行于直線.