
【題目】已知函數![]() ,
,![]() .
.
(1)求![]() 的單調區間;
的單調區間;
(2)若![]() 在
在![]() 上成立,求
上成立,求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】為響應市政府提出的以新舊動能轉換為主題的發展戰略,某公司花費100萬元成本購買了1套新設備用于擴大生產,預計該設備每年收入100萬元,第一年該設備的各種消耗成本為8萬元,且從第二年開始每年比上一年消耗成本增加8萬元.
(1)求該設備使用x年的總利潤y(萬元)與使用年數x(x∈N*)的函數關系式(總利潤=總收入﹣總成本);
(2)這套設備使用多少年,可使年平均利潤最大?并求出年平均利潤的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),過點
為參數),過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)若圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求
,求![]() 的值;
的值;
(2)求線段![]() 中點
中點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌手機廠商推出新款的旗艦機型,并在某地區跟蹤調查得到這款手機上市時間(第![]() 周)和市場占有率(
周)和市場占有率(![]() )的幾組相關數據如下表:
)的幾組相關數據如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)根據表中的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)根據上述線性回歸方程,預測在第幾周,該款旗艦機型市場占有率將首次超過![]() (最后結果精確到整數).
(最后結果精確到整數).
參考公式: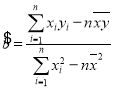 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某區“創文明城區”(簡稱“創城”)活動中,教委對本區![]() 四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
學校 |
|
|
|
|
抽查人數 | 50 | 15 | 10 | 25 |
“創城”活動中參與的人數 | 40 | 10 | 9 | 15 |
(注:參與率是指:一所學校“創城”活動中參與的人數與被抽查人數的比值)假設每名高中學生是否參與”創城”活動是相互獨立的.
(1)若該區共2000名高中學生,估計![]() 學校參與“創城”活動的人數;
學校參與“創城”活動的人數;
(2)在隨機抽查的100名高中學生中,隨機抽取1名學生,求恰好該生沒有參與“創城”活動的概率;
(3)在上表中從![]() 兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好
兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好![]() 兩校各有1人沒有參與“創城”活動的概率是多少?
兩校各有1人沒有參與“創城”活動的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,點
,點![]() 、
、![]() 分別在線段
分別在線段![]() 、
、![]() 上,且
上,且![]() ,其中
,其中![]() ,連接
,連接![]() ,延長
,延長![]() 與
與![]() 的延長線交于點
的延長線交于點![]() ,連接
,連接![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 時,求二面角
時,求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)若直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 時,求
時,求![]() 值.
值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數學建模課上,老師給大家帶來了一則新聞:“2019年8月16日上午,423米的東莞第一高樓民盈國貿中心2號樓(以下簡稱“國貿中心”)正式封頂,隨著最后一方混凝土澆筑到位,標志著東莞最高樓紀錄誕生,由東莞本地航母級企業民盈集團刷新了東莞天際線,比之前的東莞第一高樓臺商大廈高出134米.”在同學們的驚嘆中,老師提出了問題:國貿中心真有這么高嗎?我們能否運用所學知識測量驗證一下?一周后,兩個興趣小組分享了他們各自的測量方案.
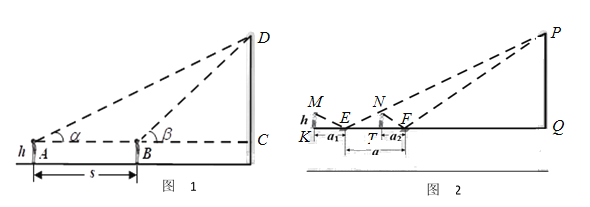
第一小組采用的是“兩次測角法”:他們在國貿中心隔壁的會展中心廣場上的![]() 點測得國貿中心頂部的仰角為
點測得國貿中心頂部的仰角為![]() ,正對國貿中心前進了
,正對國貿中心前進了![]() 米后,到達
米后,到達![]() 點,在
點,在![]() 點測得國貿中心頂部的仰角為
點測得國貿中心頂部的仰角為![]() ,然后計算出國貿中心的高度(如圖).
,然后計算出國貿中心的高度(如圖).
第二小組采用的是“鏡面反射法”:在國貿中心后面的新世紀豪園一幢11層樓(與國貿中心處于同一水平面,每層約3米)樓頂天臺上,進行兩個操作步驟:①將平面鏡置于天臺地面上,人后退至從鏡中能看到國貿大廈的頂部位置,測量出人與鏡子的距離為![]() 米;②正對國貿中心,將鏡子前移
米;②正對國貿中心,將鏡子前移![]() 米,重復①中的操作,測量出人與鏡子的距離為
米,重復①中的操作,測量出人與鏡子的距離為![]() 米.然后計算出國貿中心的高度(如圖).
米.然后計算出國貿中心的高度(如圖).
實際操作中,第一小組測得![]() 米,
米,![]() ,
,![]() ,最終算得國貿中心高度為
,最終算得國貿中心高度為![]() ;第二小組測得
;第二小組測得![]() 米,
米,![]() 米,
米,![]() 米,最終算得國貿中心高度為
米,最終算得國貿中心高度為![]() ;假設他們測量者的“眼高
;假設他們測量者的“眼高![]() ”都為
”都為![]() 米.
米.
(1)請你用所學知識幫兩個小組完成計算(參考數據:![]() ,
,![]() ,答案保留整數結果);
,答案保留整數結果);
(2)你認為哪個小組的方案更好,說出你的理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的是( )
A.![]() 是空間中的四點,若
是空間中的四點,若![]() 不能構成空間基底,則
不能構成空間基底,則![]() 共面
共面
B.已知![]() 為空間的一個基底,若
為空間的一個基底,若![]() ,則
,則![]() 也是空間的基底
也是空間的基底
C.若直線![]() 的方向向量為
的方向向量為![]() ,平面
,平面![]() 的法向量為
的法向量為![]() ,則直線
,則直線![]()
D.若直線![]() 的方向向量為
的方向向量為![]() ,平面
,平面![]() 的法向量為
的法向量為![]() ,則直線
,則直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com