
【題目】已知f(x)=x2+bx+c為偶函數,曲線y=f(x)過點(2,5),g(x)=(x+a)f(x).
(1)求曲線y=g(x)有斜率為0的切線,求實數a的取值范圍;
(2)若當x=﹣1時函數y=g(x)取得極值,確定y=g(x)的單調區間.
【答案】
(1)解:∵f(x)=x2+bx+c為偶函數,故f(﹣x)=f(x)即有
(﹣x)2+b(﹣x)+c=x2+bx+c解得b=0
又曲線y=f(x)過點(2,5),得22+c=5,有c=1
∵g(x)=(x+a)f(x)=x3+ax2+x+a從而g′(x)=3x2+2ax+1,
∵曲線y=g(x)有斜率為0的切線,故有g′(x)=0有實數解.即3x2+2ax+1=0有實數解.
此時有△=4a2﹣12≥0解得
a∈(﹣∞,﹣ ![]() ]∪[
]∪[ ![]() ,+∞)所以實數a的取值范圍:a∈(﹣∞,﹣
,+∞)所以實數a的取值范圍:a∈(﹣∞,﹣ ![]() ]∪[
]∪[ ![]() ,+∞)
,+∞)
(2)解:因x=﹣1時函數y=g(x)取得極值,故有g′(﹣1)=0即3﹣2a+1=0,解得a=2
又g′(x)=3x2+4x+1=(3x+1)(x+1)令g′(x)=0,得x1=﹣1,x2= ![]()
當x∈(﹣∞,﹣1)時,g′(x)>0,故g(x)在(﹣∞,﹣1)上為增函數
當 ![]() 時,g′(x)<0,故g(x)在(﹣1,﹣
時,g′(x)<0,故g(x)在(﹣1,﹣ ![]() )上為減函數
)上為減函數
當x∈(﹣ ![]() )時,g′(x)>0,故g(x)在
)時,g′(x)>0,故g(x)在 ![]() 上為增函數
上為增函數
【解析】(1)據偶函數的定義f(﹣x)=f(x)求出b值,將點(2,5)代入得c值,據導數在切點處的導數值為切線斜率,
有g′(x)=0有實數解,由△≥0得范圍.(2),函數在極值點處的導數值為0,導數大于0對應區間是單調遞增區間;導數小于0對應區間是單調遞減區間.
【考點精析】解答此題的關鍵在于理解導數的幾何意義的相關知識,掌握通過圖像,我們可以看出當點![]() 趨近于
趨近于![]() 時,直線
時,直線![]() 與曲線相切.容易知道,割線
與曲線相切.容易知道,割線![]() 的斜率是
的斜率是![]() ,當點
,當點![]() 趨近于
趨近于![]() 時,函數
時,函數![]() 在
在![]() 處的導數就是切線PT的斜率k,即
處的導數就是切線PT的斜率k,即![]() ,以及對利用導數研究函數的單調性的理解,了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間
,以及對利用導數研究函數的單調性的理解,了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減.
在這個區間單調遞減.


 優生樂園系列答案
優生樂園系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線x2=4y焦點為F,點A,B,C為該拋物線上不同的三點,且滿足 ![]() +
+ ![]() +
+ ![]() =
= ![]() .
.
(1)求|FA|+|FB|+|FC|;
(2)若直線AB交y軸于點D(0,b),求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,底面ABCD是邊長為1的正方形,PA⊥平面ABCD,PA=AB,M,N分別為PB,AC的中點, 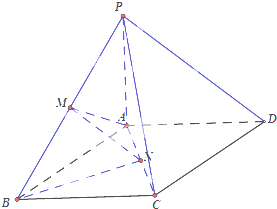
(1)求證:MN∥平面PAD;
(2)求點B到平面AMN的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,以原點為O極點,以x軸正半軸為極軸,圓C的極坐標方程為ρ=4 ![]() .
.
(1)將圓C的極坐標方程化為直角坐標方程;
(2)過點P(2,0)作斜率為1直線l與圓C交于A,B兩點,試求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系,已知點A的極坐標為( ![]() ,
, ![]() ),直線l的極坐標方程為ρcos(θ﹣
),直線l的極坐標方程為ρcos(θ﹣ ![]() )=a,且點A在直線l上,
)=a,且點A在直線l上,
(1)求a的值及直線l的直角坐標方程;
(2)圓C的參數方程為 ![]() (α為參數),試判斷直線l與圓C的位置關系.
(α為參數),試判斷直線l與圓C的位置關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com