
設函數f (x)=x3-4x+a,0<a<2.若f (x)的三個零點為x1,x2,x3,且x1<x2<x3,則
| A.x1>-1 | B.x2<0 | C.x2>0 | D.x3>2 |
C
解析試題分析:利用導數研究函數的單調性,利用導數求函數的極值,再根據f (x)的三個零點為x1,x2,x3,且x1<x2<x3,求得各個零點所在的區間,從而得出結論.
∵函數f (x)=x3-4x+a,0<a<2,
∴f′(x)=3x2-4.令f′(x)=0,得 x=±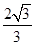
當x<-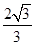 時,則f′(x)>0;在(-
時,則f′(x)>0;在(-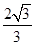 ,
,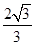 )上,f′(x)<0;在(
)上,f′(x)<0;在(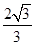 ,+
,+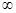 ),f′(x)>0.故可知函數零點,再由f (x)的三個零點為x1,x2,x3,且x1<x2<x3,
),f′(x)>0.故可知函數零點,再由f (x)的三個零點為x1,x2,x3,且x1<x2<x3,
x1<-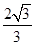 ,,-
,,-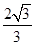 < x2<
< x2<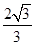 , x3>
, x3>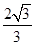 且可知根據f(0)=a>0,f(
且可知根據f(0)=a>0,f(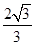 )<0因此可知選C.
)<0因此可知選C.
考點:函數零點
點評:本題主要考查函數的零點的定義,函數的零點與方程的根的關系,利用導數研究函數的單調性,利用導數求函數的極值,屬于中檔題.


 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:高中數學 來源: 題型:單選題
函數y=f(x),x∈D,若存在常數C,對任意的xl∈D,仔在唯一的x2∈D,使得 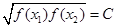 ,則稱函數f(x)在D上的幾何平均數為C.已知f(x)=x3,x∈[1,2],則函數f(x)=x3在[1,2]上的幾何平均數為
,則稱函數f(x)在D上的幾何平均數為C.已知f(x)=x3,x∈[1,2],則函數f(x)=x3在[1,2]上的幾何平均數為
A. B.2 C.4 D. 2
B.2 C.4 D. 2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com