Question

18．在平面直角坐標系中，A、B分別是x軸和y軸上的動點，若以AB為直徑的圓C與直線2x+y-4=0相切，則圓C面積的最小值為$\frac{4π}{5}$．

Answer 1

分析 如圖，設AB的中點為C，坐標原點為O，圓半徑為r，由已知得|OC|=|CE|=r，過點O作直線2x+y-4=0的垂直線段OF，交AB于D，交直線2x+y-4=0于F，則當D恰為AB中點時，圓C的半徑最小，即面積最小．

解答 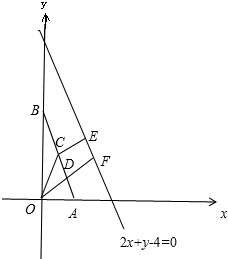解：如圖，設AB的中點為C，坐標原點為O，圓半徑為r，
由已知得|OC|=|CE|=r，
過點O作直線2x+y-4=0的垂直線段OF，
交AB于D，交直線2x+y-4=0于F，
則當D恰為OF中點時，圓C的半徑最小，即面積最小．
此時圓的直徑為O（0，0）到直線2x+y-4=0的距離為：
d=$\frac{|-4|}{\sqrt{4+1}}$=$\frac{4}{\sqrt{5}}$，
此時r=$\frac{1}{2}d$=$\frac{2}{\sqrt{5}}$
∴圓C的面積的最小值為：S_min=π×（$\frac{2}{\sqrt{5}}$）²=$\frac{4π}{5}$．
故答案為$\frac{4π}{5}$．

點評 本題主要考查了直線與圓的位置關系，考查圓的面積的最小值的求法，是中檔題，解題時要認真審題，注意數形結合思想的合理運用．