是否存在一個三角形同時具有以下性質:
(1)三邊是連續的三個自然數
(2)最大角是最小角的2倍.
【答案】
分析:設三角形三邊是連續的三個自然n-1,n,n+1,三個角分別為α,π-3α,2α,由正弦定理求得cosα=

,
再由余弦定理可得 (n-1)
2=(n+1)
2+n
2-2(n+1)n•
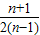
,求得n=5,從而得出結論.
解答:解:設三角形三邊是連續的三個自然n-1,n,n+1,三個角分別為α,π-3α,2α,
由正弦定理可得
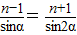
,∴cosα=
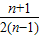
.
再由余弦定理可得 (n-1)
2=(n+1)
2+n
2-2(n+1)n•cosα,即 (n-1)
2=(n+1)
2+n
2-2(n+1)n•

,
化簡可得n
2-5n=0,∴n=5. 此時,三角形的三邊分別為:4,5,6,可以檢驗最大角是最小角的2倍.
綜上,存在一個三角形三邊長分別為 4,5,6,且最大角是最小角的2倍.
點評:本題考查正弦定理、余弦定理的應用,求得n
2-5n=0,是解題的難點,屬于中檔題.

 ,
,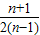 ,求得n=5,從而得出結論.
,求得n=5,從而得出結論.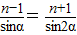 ,∴cosα=
,∴cosα=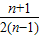 .
. ,
,
