
【題目】在某海濱城市附近海面有一臺風,據監測,當前臺風中心位于城市A(看做一點)的東偏南![]() 角方向
角方向![]() ,300 km的海面P處,并以20km / h的速度向西偏北45°方向移動.臺風侵襲的范圍為圓形區域,當前半徑為60 km,并以10km / h的速度不斷增大.
,300 km的海面P處,并以20km / h的速度向西偏北45°方向移動.臺風侵襲的范圍為圓形區域,當前半徑為60 km,并以10km / h的速度不斷增大.
(1) 問10小時后,該臺風是否開始侵襲城市A,并說明理由;
(2) 城市A受到該臺風侵襲的持續時間為多久?
【答案】(1)否;(2)![]() 小時.
小時.
【解析】
建立直角坐標系,則城市A(0,0),當前臺風中心![]() ,設t小時后臺風中心P的坐標為(x,y),由題意建立方程組,能求出10小時后,該臺風還沒有開始侵襲城市A.(2)t小時后臺風侵襲的范圍可視為以
,設t小時后臺風中心P的坐標為(x,y),由題意建立方程組,能求出10小時后,該臺風還沒有開始侵襲城市A.(2)t小時后臺風侵襲的范圍可視為以![]() 為圓心,60+10t為半徑的圓,由此利用圓的性質能求出結果.
為圓心,60+10t為半徑的圓,由此利用圓的性質能求出結果.
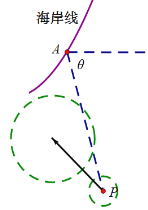
(1)如圖建立直角坐標系, 則城市![]() ,當前臺風中心
,當前臺風中心![]() ,
,

設t小時后臺風中心P的坐標為![]() ,則
,則![]() ,
,
此時臺風的半徑為![]() ,
,
10小時后,![]() km,臺風的半徑為
km,臺風的半徑為![]() 160km,
160km,
因為![]() ,故10小時后,該臺風還沒有開始侵襲城市A.
,故10小時后,該臺風還沒有開始侵襲城市A.
(2)因此,t小時后臺風侵襲的范圍可視為以
![]() 為圓心,
為圓心,![]() 為半徑的圓,
為半徑的圓,
若城市A受到臺風侵襲,則![]()
![]() ,即
,即![]() ,
,
解得![]()
答:該城市受臺風侵襲的持續時間為12小時.


科目:高中數學 來源: 題型:
【題目】設拋物線![]() 的焦點為F,已知直線
的焦點為F,已知直線![]() 與拋物線C交于A,B兩點(A,B兩點分別在
與拋物線C交于A,B兩點(A,B兩點分別在![]() 軸的上、下方).
軸的上、下方).
(1)求證:![]() ;
;
(2)已知弦長![]() ,試求:過A,B兩點,且與直線
,試求:過A,B兩點,且與直線![]() 相切的圓D的方程.
相切的圓D的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解甲、乙兩種離子在小鼠體內的殘留程度,進行如下試驗:將200只小鼠隨機分成![]() 兩組,每組100只,其中
兩組,每組100只,其中![]() 組小鼠給服甲離子溶液,
組小鼠給服甲離子溶液,![]() 組小鼠給服乙離子溶液.每只小鼠給服的溶液體積相同、摩爾濃度相同.經過一段時間后用某種科學方法測算出殘留在小鼠體內離子的百分比.根據試驗數據分別得到如下直方圖:
組小鼠給服乙離子溶液.每只小鼠給服的溶液體積相同、摩爾濃度相同.經過一段時間后用某種科學方法測算出殘留在小鼠體內離子的百分比.根據試驗數據分別得到如下直方圖:

記![]() 為事件:“乙離子殘留在體內的百分比不低于
為事件:“乙離子殘留在體內的百分比不低于![]() ”,根據直方圖得到
”,根據直方圖得到![]() 的估計值為
的估計值為![]() .
.
(1)求乙離子殘留百分比直方圖中![]() 的值;
的值;
(2)分別估計甲、乙離子殘留百分比的平均值(同一組中的數據用該組區間的中點值為代表).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方形![]() 中,
中,![]() ,
,![]() 分別為棱
分別為棱![]() 和棱
和棱![]() 的中點,則下列說法正確的是( )
的中點,則下列說法正確的是( )
A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() 截正方體所得截面為等腰梯形
截正方體所得截面為等腰梯形
C.![]() 平面
平面![]() D.異面直線
D.異面直線![]() 與
與![]() 所成的角為60°
所成的角為60°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列是合情推理的是( )
①由正三角形的性質類比出正三棱錐的有關性質;
②由正方形矩形的內角和是![]() ,歸納出所有四邊形的內角和都是;
,歸納出所有四邊形的內角和都是;
③三角形內角和是![]() ,四邊形內角和是
,四邊形內角和是![]() ,五邊形內角和是
,五邊形內角和是![]() ,由此得出凸
,由此得出凸![]() 邊形內角和是
邊形內角和是![]() ;
;
④小李某次數學考試成績是90分,由此推出小李的全班同學這次數學考試的成績都是90分.
A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l的方程為3x+4y-12=0,求直線l′的方程,使得:
(1)l′與l平行且過點(-1,3);
(2)l′與l垂直且l′與兩坐標軸圍成的三角形的面積為4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017-2018學年安徽省六安市第一中學高三上學期第二次月考)已知函數![]() 是偶函數.
是偶函數.
(1)求![]() 的值;
的值;
(2)若函數![]() 的圖象與直線
的圖象與直線![]() 沒有交點,求
沒有交點,求![]() 的取值范圍;
的取值范圍;
(3)若函數![]() ,是否存在實數
,是否存在實數![]() 使得
使得![]() 的最小值為0,若存在,求出
的最小值為0,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com