
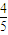 ?若存在,求出線段CQ的長;若不存在,請說明理由.
?若存在,求出線段CQ的長;若不存在,請說明理由.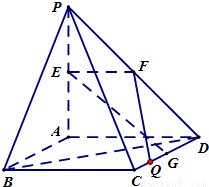
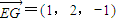 ,
,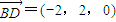 的坐標(biāo),利用異面直線EG與BD所成角公式求出異面直線EG與BD所成角大小即可;
的坐標(biāo),利用異面直線EG與BD所成角公式求出異面直線EG與BD所成角大小即可;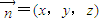 ,再點(diǎn)A到平面EFQ的距離,求出x,若出現(xiàn)矛盾,則說明假設(shè)不成立,即不存在;否則存在.
,再點(diǎn)A到平面EFQ的距離,求出x,若出現(xiàn)矛盾,則說明假設(shè)不成立,即不存在;否則存在. 解:(1)以點(diǎn)A為坐標(biāo)原點(diǎn),射線AB,AD,AZ分別為x軸、y軸、z軸的正半軸建立空間直角坐標(biāo)系如圖示,點(diǎn)E(0,0,1)、G(1,2,0)、B(2,0,0)、D(0,2,0),
解:(1)以點(diǎn)A為坐標(biāo)原點(diǎn),射線AB,AD,AZ分別為x軸、y軸、z軸的正半軸建立空間直角坐標(biāo)系如圖示,點(diǎn)E(0,0,1)、G(1,2,0)、B(2,0,0)、D(0,2,0),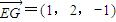 ,
,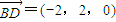 .
.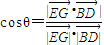 =
=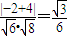 ,
,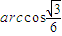 .
.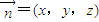 ,
,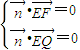 得到y(tǒng)=0,z=xx,取x=1,
得到y(tǒng)=0,z=xx,取x=1,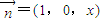 ,
,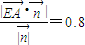 ,
,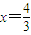 ,
,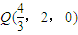 即
即 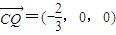 ,
,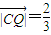 .
. .
.


| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
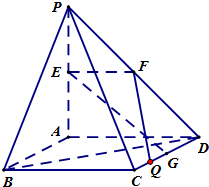 (理)如圖,PA⊥平面ABCD,四邊形ABCD是正方形,PA=AD=2,點(diǎn)E、F、G分別為線段PA、PD和CD的中點(diǎn).
(理)如圖,PA⊥平面ABCD,四邊形ABCD是正方形,PA=AD=2,點(diǎn)E、F、G分別為線段PA、PD和CD的中點(diǎn).| 4 |
| 5 |
| e |
| e |
| π |
| 2 |
| a |
| 1 |
| 2 |
| e |
| ||
| 2 |
| e |
| e |
| e |
| a |
| a |
| b |
| e |
| e |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (2011•崇明縣二模)(理)如圖,PA⊥平面ABCD,四邊形ABCD是正方形,PA=AD=2,點(diǎn)E、F、G分別為線段PA、PD和CD的中點(diǎn).
(2011•崇明縣二模)(理)如圖,PA⊥平面ABCD,四邊形ABCD是正方形,PA=AD=2,點(diǎn)E、F、G分別為線段PA、PD和CD的中點(diǎn).| 4 | 5 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年上海普陀區(qū)高考數(shù)學(xué)三模試卷(文理合卷)(解析版) 題型:解答題
 ?若存在,求出線段CQ的長;若不存在,請說明理由.
?若存在,求出線段CQ的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年上海市普陀區(qū)高考數(shù)學(xué)二模試卷(文理合卷)(解析版) 題型:解答題
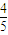 ?若存在,求出線段CQ的長;若不存在,請說明理由.
?若存在,求出線段CQ的長;若不存在,請說明理由.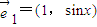 ,
,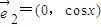 ,其中
,其中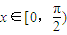 ,且向量
,且向量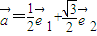 .
.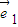 和
和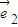 都為單位向量時,求
都為單位向量時,求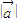 ;
;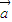 和向量
和向量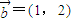 共線,求向量
共線,求向量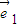 和
和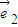 的夾角.
的夾角.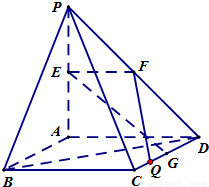
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com