
【題目】設函數![]() .
.
(1)求函數![]() 的單調區間和極值;
的單調區間和極值;
(2)若存在![]() 滿足
滿足![]() ,證明
,證明![]() 成立.
成立.
【答案】(1)當![]() 時,
時, ![]() 在
在![]() 上單調遞增沒有極值;當
上單調遞增沒有極值;當![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 在
在![]() 上單調遞減,極小值為
上單調遞減,極小值為![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
(1)對函數進行求導得![]() ,分為
,分為![]() 和
和![]() 兩種情形判別導數與0的關系即可得結果;
兩種情形判別導數與0的關系即可得結果;
(2)先得出![]() ,結合(1)知
,結合(1)知![]() ,設
,設![]() ,構造函數
,構造函數![]() ,通過導數判斷出
,通過導數判斷出![]() 的單調性,可得出
的單調性,可得出![]() ,結合(1)中的單調性即可得出結果.
,結合(1)中的單調性即可得出結果.
(1)由![]() 得
得![]()
當![]() 時,
時,![]() 從而得
從而得![]() 在
在![]() 上單調遞增沒有極值;
上單調遞增沒有極值;
當![]() 時,
時,![]() 得
得![]() ;
;
![]() 得
得![]() ;
;![]() 得
得![]() ;
;
![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 在
在![]() 上單調遞減,
上單調遞減,
此時有極小值![]() ,無極大值.
,無極大值.
(2)由![]() 得:
得:![]() ,從而得
,從而得![]()
由(1)知當![]() 時,
時,![]() 從而得
從而得![]() 在
在![]() 上單調遞增,所以此時不成立
上單調遞增,所以此時不成立
可知此時![]() ,由于
,由于![]() 的極小值點為
的極小值點為![]() ,可設
,可設![]()
設![]()
![]()
![]()
![]() ,僅當
,僅當![]() 時取得“
時取得“![]() ”
”
所以![]() 在
在![]() 為單調遞增函數且
為單調遞增函數且![]()
當![]() ,時有
,時有![]() ,即
,即![]()
又由![]() ,所以
,所以![]()
又由(1)知![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]() ,
,![]()
所以![]() 從而得證
從而得證![]() 成立.
成立.


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數學 來源: 題型:
【題目】兩城市![]() 和
和![]() 相距
相距![]() ,現計劃在兩城市外以
,現計劃在兩城市外以![]() 為直徑的半圓
為直徑的半圓![]() 上選擇一點
上選擇一點![]() 建造垃圾處理場,其對城市的影響度與所選地點到城市的距離有關,對城
建造垃圾處理場,其對城市的影響度與所選地點到城市的距離有關,對城![]() 和城
和城![]() 的總影響度為城
的總影響度為城![]() 和城
和城![]() 的影響度之和,記
的影響度之和,記![]() 點到城
點到城![]() 的距離為
的距離為![]() ,建在
,建在![]() 處的垃圾處理場對城
處的垃圾處理場對城![]() 和城
和城![]() 的總影響度為
的總影響度為![]() ,統計調查表明:垃圾處理場對城
,統計調查表明:垃圾處理場對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比,比例系數為4,對城
的距離的平方成反比,比例系數為4,對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比,比例系數為
的距離的平方成反比,比例系數為![]() ,當垃圾處理場建在
,當垃圾處理場建在![]() 的中點時,對城
的中點時,對城![]() 和城
和城![]() 的總影響度為0.065;
的總影響度為0.065;
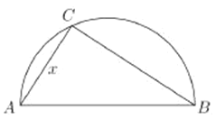
(1)將![]() 表示成
表示成![]() 的函數;
的函數;
(2)判斷![]() 上是否存在一點,使建在此處的垃圾處理場對城
上是否存在一點,使建在此處的垃圾處理場對城![]() 和城
和城![]() 的總影響度最小?若存在,求出該點到城
的總影響度最小?若存在,求出該點到城![]() 的距離;若不存在,說明理由;
的距離;若不存在,說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某摩托車生產企業,上年度生產摩托車的投入成本為1萬元/輛,出廠價為1.2萬元/輛,年銷售量為1000輛.本年度為適應市場需求,計劃提高產品檔次,適度增加投入成本.若每輛車投入成本增加的比例為x(0<x<1),則出廠價相應的提高比例為0.75x,同時預計年銷售量增加的比例為0.6x.已知年利潤=(出廠價﹣投入成本)×年銷售量.
(1)寫出本年度預計的年利潤y與投入成本增加的比例x的關系式;
(2)為使本年度的年利潤比上年有所增加,問投入成本增加的比例x應在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數對序列![]() 、
、![]() 、
、![]() 、
、![]() ,記
,記![]() ,
,![]() ,其中
,其中![]() 表示
表示![]() 和
和![]() 兩個數中最大的數.
兩個數中最大的數.
(1)對于數對序列![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)記![]() 為
為![]() 、
、![]() 、
、![]() 、
、![]() 四個數中最小值,對于由兩個數對
四個數中最小值,對于由兩個數對![]() 、
、![]() 組成的數對序列
組成的數對序列![]() 、
、![]() 和
和![]() 、
、![]() ,試分別對
,試分別對![]() 和
和![]() 的兩種情況比較
的兩種情況比較![]() 和
和![]() 的大小;
的大小;
(3)在由![]() 個數對
個數對![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 組成的所有數對序列中,寫出一個數對序列
組成的所有數對序列中,寫出一個數對序列![]() 使
使![]() 最小,并寫出
最小,并寫出![]() 的值.(只需寫出結論)
的值.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知曲線![]() ,曲線
,曲線![]() ,P是平面上一點,若存在過點P的直線與
,P是平面上一點,若存在過點P的直線與![]() 都有公共點,則稱P為“C1—C2型點”.
都有公共點,則稱P為“C1—C2型點”.
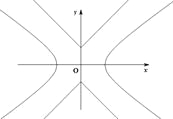
(1)在正確證明![]() 的左焦點是“C1—C2型點”時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
的左焦點是“C1—C2型點”時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
(2)設直線![]() 與
與![]() 有公共點,求證
有公共點,求證![]() ,進而證明原點不是“C1—C2型點”;
,進而證明原點不是“C1—C2型點”;
(3)求證:圓![]() 內的點都不是“C1—C2型點”.
內的點都不是“C1—C2型點”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為![]() (其中
(其中![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若點![]() 在直線
在直線![]() 上,且
上,且![]() ,求直線
,求直線![]() 的斜率;
的斜率;
(2)若![]() ,求曲線
,求曲線![]() 上的點到直線
上的點到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com