定義在R上的函數y=f(x)是增函數,且函數y=f(x-2)的圖象關于(2,0)成中心對稱,若s,t滿足不等式f(s2-4s)≥-f(4t-t2),若-2≤s≤2時,則3t+s的最大值為 .
【答案】
分析:根據函數圖象平移的公式結合奇偶性定義,可得函數y=f(x)是奇函數.因此將f(s
2-4s)≥-f(4t-t
2)變形,化簡整理得到(s-t)(s+t-4)≥0,以s為橫坐標、t為縱坐標建立坐標系,結合-2≤s≤2作出不等式組表示的平面區域如圖所示.再將z=3t+s對應的直線l進行平移,即可得到當s=-2,t=6時,3t+s的最大值為16.
解答:解:∵y=f(x-2)的圖象由y=f(x)函數圖象向右移2個單位而得
∴由y=f(x-2)圖象關于(2,0)點對稱,可得函數y=f(x)的圖象關于(0,0)點對稱.
由此可得函數y=f(x)是奇函數
∴f(4t-t
2)=-f(t
2-4t)
∵f(s
2-4s)≥-f(4t-t
2),∴f(s
2-4s)≥f(t
2-4t)
又∵y=f(x)函數是增函數,
∴s
2-4s≥t
2-4t,移項得:s
2-4s-t
2+4t≥0
化簡整理可得:(s-t)(s+t-4)≥0
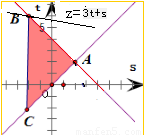
以s為橫坐標、t為縱坐標,建立如圖直角坐標系,
則不等式
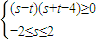
表示的平面區域如圖所示
即△ABC及其內部,其中A(2,2),B(-2,6),C(-2,-2)
設z=F(s,t)=3t+s,將直線l:z=3t+s進行平移,
可得當l經過點B時,z達到最大值
∴z
max=F(s,t)=3×6+(-2)=16
故答案為:16
點評:本題以函數的奇偶性和不等式等價變形為載體,考查了函數的圖象與基本性質、二元一次不等式表示的平面區域和簡單的線性規劃等知識,屬于中檔題.


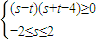 表示的平面區域如圖所示
表示的平面區域如圖所示
