
 ,從而n≥3,故
,從而n≥3,故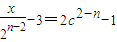 或
或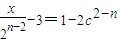 ,當n≥3時,
,當n≥3時,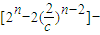
 =
=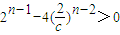 ,于是a1+a2=22+23,a3+a4=23+24,從而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.從而得出數列a2n-1+a2n構成以12為首項,2為公比的等比數列.
,于是a1+a2=22+23,a3+a4=23+24,從而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.從而得出數列a2n-1+a2n構成以12為首項,2為公比的等比數列.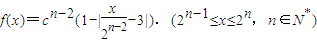 的極大值點為pn(xn,yn).由
的極大值點為pn(xn,yn).由 =
=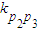 (k表示直線的斜率),得c=2或c=1.分別求出當c=2時的拋物線方程,以及當c=4,
(k表示直線的斜率),得c=2或c=1.分別求出當c=2時的拋物線方程,以及當c=4,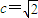 時,拋物線方程即可.
時,拋物線方程即可.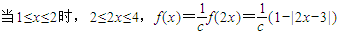 ;
;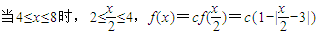 ;
;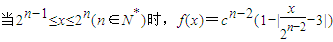 .
.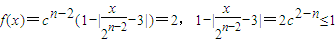 ,(2)
,(2)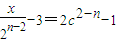 或
或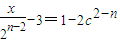 ,于是,
,于是,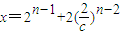 或
或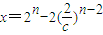 .
.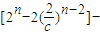
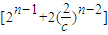 =
=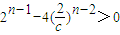
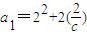 ,
,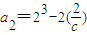 ,
,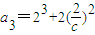 ,
,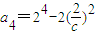 ,于是a1+a2=22+23,a3+a4=23+24,從而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.
,于是a1+a2=22+23,a3+a4=23+24,從而a2n-1+a2n=2n+1+2n+2=12•2n-1,n∈N*.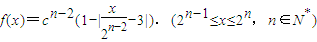 的極大值點為pn(xn,yn).
的極大值點為pn(xn,yn).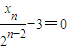 ,即xn=3•2n-2時,yn=cn-2,故pn(3•2n-2,cn-2).
,即xn=3•2n-2時,yn=cn-2,故pn(3•2n-2,cn-2).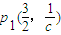 ,p2(3,1),p3(6,c).
,p2(3,1),p3(6,c).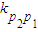 =
=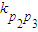 (k表示直線的斜率),得c=2或c=1.
(k表示直線的斜率),得c=2或c=1.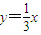 上;
上;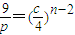 對n∈N*恒成立,從而c=4,p=9,拋物線方程為x2=9y;
對n∈N*恒成立,從而c=4,p=9,拋物線方程為x2=9y;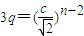 對n∈N*恒成立,從而
對n∈N*恒成立,從而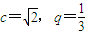 ,拋物線方程為y2=
,拋物線方程為y2= x(14分)
x(14分)

科目:高中數學 來源: 題型:
| A、增函數 | B、先增后減函數 | C、減函數 | D、與a,b有關,不能確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| A、[-10,2] | B、[-12,0] | C、[-12,2] | D、與a,b有關,不能確定 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com