從點P(2,3)向圓(x-1)2+(y-1)2=1引切線,則切線方程為 .
【答案】
分析:先看切線的斜率存在時,設出切線的方程,進而利用點到直線的距離求得圓心到切線的距離,進而求得k,切線的方程可得;再看切線的斜率不存在時,切線方程可得.
解答:解:(1)若切線的斜率存在,可設切線的方程為y-3=k(x-2)即kx-y-2k+3=0
則圓心到切線的距離
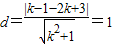
解得
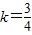
故切線的方程為3x-4y+6=0
(2)若切線的斜率不存在,切線方程為x=2,此時直線也與圓相切.
綜上所述,過P點的切線的方程為:3x-4y+6=0和x=2.
故答案為x=2或3x-4y+6=0
點評:本題主要考查了直線與圓的位置的關系,點到直線的距離公式.考查了學生數形結合的思想的運用和基本的運算能力.

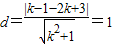
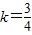


 閱讀快車系列答案
閱讀快車系列答案