
【題目】在邊長為2的菱形![]() 中,
中,![]() ,將菱形
,將菱形![]() 沿對角線
沿對角線![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,則所得三棱錐
,則所得三棱錐![]() 的外接球表面積為( )
的外接球表面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中數學 來源: 題型:
【題目】為了解甲、乙兩種產品的質量,從中分別隨機抽取了10件樣品,測量產品中某種元素的含量(單位:毫克),如圖所示是測量數據的莖葉圖.規定:當產品中的此中元素的含量不小于18毫克時,該產品為優等品.
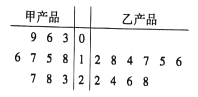
(1)試用樣品數據估計甲、乙兩種產品的優等品率;
(2)從乙產品抽取的10件樣品中隨機抽取3件,求抽到的3件樣品中優等品數![]() 的分布列及其數學期望
的分布列及其數學期望![]() ;
;
(3)從甲產品抽取的10件樣品中有放回地隨機抽取3件,也從乙產品抽取的10件樣品中有放回地隨機抽取3件;抽到的優等品中,記“甲產品恰比乙產品多2件”為事件![]() ,求事件
,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知拋物線
中,已知拋物線![]() ,過點
,過點![]() 的直線
的直線![]() 交拋物線于
交拋物線于![]() ,
,![]() ,
,![]() ,
,![]() 兩點.當
兩點.當![]() 垂直于
垂直于![]() 軸時,
軸時,![]() 的面積為
的面積為![]() .
.
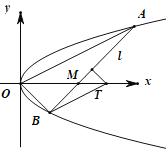
0
(1)求拋物線的方程:
(2)設線段![]() 的垂直平分線交
的垂直平分線交![]() 軸于點
軸于點![]() .
.
①證明:![]() 為定值:
為定值:
②若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方體![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一條線段,且
上的一條線段,且![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是棱
是棱![]() 上的動點,則
上的動點,則
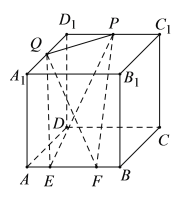
①四面體![]() 的體積為定值
的體積為定值
②直線![]() 到平面
到平面![]() 的距離為定值
的距離為定值
③點![]() 到直線
到直線![]() 的距離為定值
的距離為定值
④直線![]() 與平面
與平面![]() 所成的角為定值
所成的角為定值
其中正確結論的編號是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的上頂點為
的上頂點為![]() ,左,右焦點分別為
,左,右焦點分別為![]() ,
,![]() ,
,![]() 的面積為
的面積為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() .
.![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于點
交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.![]() ,且
,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知曲線![]() (
(![]() 為參數),直線
為參數),直線![]() (
(![]() 為參數,
為參數, ![]() ),直線
),直線![]() 與曲線
與曲線![]() 相切于點
相切于點![]() ,以坐標原點
,以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程及點
的極坐標方程及點![]() 的極坐標;
的極坐標;
(2)曲線![]() 的直角坐標方程為
的直角坐標方程為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于在
交于在![]() ,
,![]() 兩點,記
兩點,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的普通方程為
的普通方程為![]() ,以原點
,以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(I)求![]() 的參數方程與
的參數方程與![]() 的直角坐標方程;
的直角坐標方程;
(II)射線![]() 與
與![]() 交于異于極點的點
交于異于極點的點![]() ,與
,與![]() 的交點為
的交點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A是以BC為直徑的圓O上異于B,C的動點,P為平面ABC外一點,且平面PBC⊥平面ABC,BC=3,PB=2![]() ,PC
,PC![]() ,則三棱錐P﹣ABC外接球的表面積為______.
,則三棱錐P﹣ABC外接球的表面積為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年春節期間,我國高速公路繼續執行“節假日高速公路免費政策”某路橋公司為掌握春節期間車輛出行的高峰情況,在某高速公路收費點記錄了大年初三上午9:20~10:40這一時間段內通過的車輛數,統計發現這一時間段內共有600輛車通過該收費點,它們通過該收費點的時刻的頻率分布直方圖如下圖所示,其中時間段9:20~9:40記作區間![]() ,9:40~10:00記作
,9:40~10:00記作![]() ,10:00~10:20記作
,10:00~10:20記作![]() ,10:20~10:40記作
,10:20~10:40記作![]() .例如:10點04分,記作時刻64.
.例如:10點04分,記作時刻64.
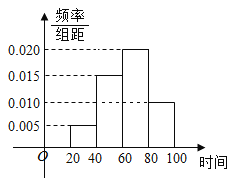
(1)估計這600輛車在9:20~10:40時間段內通過該收費點的時刻的平均值(同一組中的數據用該組區間的中點值代表);
(2)為了對數據進行分析,現采用分層抽樣的方法從這600輛車中抽取10輛,再從這10輛車中隨機抽取4輛,設抽到的4輛車中,在9:20~10:00之間通過的車輛數為X,求X的分布列與數學期望;
(3)由大數據分析可知,車輛在每天通過該收費點的時刻T服從正態分布![]() ,其中
,其中![]() 可用這600輛車在9:20~10:40之間通過該收費點的時刻的平均值近似代替,
可用這600輛車在9:20~10:40之間通過該收費點的時刻的平均值近似代替,![]() 可用樣本的方差近似代替(同一組中的數據用該組區間的中點值代表),已知大年初五全天共有1000輛車通過該收費點,估計在9:46~10:40之間通過的車輛數(結果保留到整數).
可用樣本的方差近似代替(同一組中的數據用該組區間的中點值代表),已知大年初五全天共有1000輛車通過該收費點,估計在9:46~10:40之間通過的車輛數(結果保留到整數).
參考數據:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com