設輪船A有兩個發動機,輪船B有四個發動機,如果半數或半數以上的發動機沒有故障,輪船就能夠安全航行,現設每個發動機發生故障的概率P是t的函數:P=1-e-λt(其中t為發動機啟動后所經歷的時間,λ為正常數).每個發動機工作相互獨立.
(1)分別求出輪船A,B安全航行的概率(用P表示);
(2)根據時間t的變化,比較輪船A和輪船B哪一個更能安全航行?(除發動機發生故障外,不考慮其他因素).
【答案】
分析:(1)記輪船A,B安全航行為事件M、N,分析可得輪船A安全航行,即A的兩個發動機中至少有一個正常工作,輪船B安全航行,即B的四個發動機中至少有二個正常工作,其對立事件B的四個發動機全部故障或只有一個正常工作,由相互獨立事件概率的乘法公式,計算可得答案;
(2)由(1)的結論,做差可得:p(M)-p(N)=(1-p
2)-(1+3p
4-4p
3)=-p
2(p-1)(3p-1),分①p<

,②p=

,③p>

,三種情況討論,分析p(M)與p(N)的大小,進而可得答案.
解答:解:(1)記輪船A,B安全航行為事件M、N,
輪船A安全航行,即A的兩個發動機中至少有一個正常工作,則其對立事件為A的兩個發動機都不能正常工作,
則P(M)=1-p
2,
輪船B安全航行,即B的四個發動機中至少有二個正常工作,其對立事件B的四個發動機全部故障或只有一個正常工作,
則P(N)=1-p
4-C
41p
3(1-p)=1+3p
4-4p
3,
(2)p(M)-p(N)=(1-p
2)-(1+3p
4-4p
3)=-p
2(p-1)(3p-1),
①當p<

時,即1-e
-λt<

,解可得t<
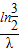
時,p(M)<p(N),輪船B能安全航行,
②當p=

時,即1-e
-λt=

,解可得t=
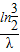
時,p(M)=p(N),輪船A、B一樣安全航行,
③當p>

時,即1-e
-λt>

,解可得t>
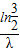
時,p(M)>p(N),輪船A更能安全航行,
答:當p<

時,輪船B能安全航行,當p=

時,輪船A、B一樣安全航行,當p>

時,輪船A更能安全航行.
點評:本題考查概率的應用,關鍵是熟練運用相互獨立事件概率乘法公式,用p表示出A、B正常航行的概率.

 ,②p=
,②p= ,③p>
,③p> ,三種情況討論,分析p(M)與p(N)的大小,進而可得答案.
,三種情況討論,分析p(M)與p(N)的大小,進而可得答案. 時,即1-e-λt<
時,即1-e-λt< ,解可得t<
,解可得t<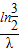 時,p(M)<p(N),輪船B能安全航行,
時,p(M)<p(N),輪船B能安全航行, 時,即1-e-λt=
時,即1-e-λt= ,解可得t=
,解可得t=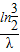 時,p(M)=p(N),輪船A、B一樣安全航行,
時,p(M)=p(N),輪船A、B一樣安全航行, 時,即1-e-λt>
時,即1-e-λt> ,解可得t>
,解可得t>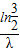 時,p(M)>p(N),輪船A更能安全航行,
時,p(M)>p(N),輪船A更能安全航行, 時,輪船B能安全航行,當p=
時,輪船B能安全航行,當p= 時,輪船A、B一樣安全航行,當p>
時,輪船A、B一樣安全航行,當p> 時,輪船A更能安全航行.
時,輪船A更能安全航行.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案