
【題目】目前,中國有三分之二的城市面臨“垃圾圍城”的窘境. 我國的垃圾處理多采用填埋的方式,占用上萬畝土地,并且嚴重污染環境. 垃圾分類把不易降解的物質分出來,減輕了土地的嚴重侵蝕,減少了土地流失. 2020年5月1日起,北京市將實行生活垃圾分類,分類標準為廚余垃圾、可回收物、有害垃圾和其它垃圾四類 .生活垃圾中有30%~40%可以回收利用,分出可回收垃圾既環保,又節約資源. 如:回收利用1噸廢紙可再造出0.8噸好紙,可以挽救17棵大樹,少用純堿240千克,降低造紙的污染排放75%,節省造紙能源消耗40%~50%.
現調查了北京市5個小區12月份的生活垃圾投放情況,其中可回收物中廢紙和塑料品的投放量如下表:
|
|
|
|
| |
廢紙投放量(噸) | 5 | 5.1 | 5.2 | 4.8 | 4.9 |
塑料品投放量(噸) | 3.5 | 3.6 | 3.7 | 3.4 | 3.3 |
(Ⅰ)從![]() 這5個小區中任取1個小區,求該小區12月份的可回收物中,廢紙投放量超過5噸且塑料品投放量超過3.5噸的概率;
這5個小區中任取1個小區,求該小區12月份的可回收物中,廢紙投放量超過5噸且塑料品投放量超過3.5噸的概率;
(Ⅱ)從![]() 這5個小區中任取2個小區,記
這5個小區中任取2個小區,記![]() 為12月份投放的廢紙可再造好紙超過4噸的小區個數,求
為12月份投放的廢紙可再造好紙超過4噸的小區個數,求![]() 的分布列及期望.
的分布列及期望.
 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 在平面直角坐標系
在平面直角坐標系![]() 下的參數方程為
下的參數方程為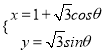 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的普通方程及極坐標方程;
的普通方程及極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() :
: ![]() 與曲線
與曲線![]() 交于點
交于點![]() 與直線
與直線![]() 交于點
交于點![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
在某次考試中,從甲乙兩個班各抽取10名學生的數學成績進行統計分析,兩個班成績的莖葉圖如圖所示,成績不小于90分的為及格.
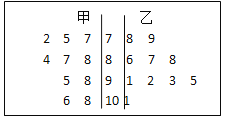
(1)用樣本估計總體,請根據莖葉圖對甲乙兩個班級的成績進行比較.
(2)求從甲班10名學生和乙班10名學生中各抽取一人,已知有人及格的條件下乙班同學不及格的概率;
(3)從甲班10人中抽取一人,乙班10人中抽取二人,三人中及格人數記為X,求X的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有人收集了七月份的日平均氣溫![]() (攝氏度)與某次冷飲店日銷售額
(攝氏度)與某次冷飲店日銷售額![]() (百元)的有關數據,為分析其關系,該店做了五次統計,所得數據如下:
(百元)的有關數據,為分析其關系,該店做了五次統計,所得數據如下:
日平均氣溫 | 31 | 32 | 33 | 34 | 35 |
日銷售額 | 5 | 6 | 7 | 8 | 10 |
由資料可知,![]() 關于
關于![]() 的線性回歸方程是
的線性回歸方程是![]() ,給出下列說法:
,給出下列說法:
①![]() ;
;
②日銷售額![]() (百元)與日平均氣溫
(百元)與日平均氣溫![]() (攝氏度)成正相關;
(攝氏度)成正相關;
③當日平均氣溫為![]() 攝氏度時,日銷售額一定為
攝氏度時,日銷售額一定為![]() 百元.
百元.
其中正確說法的序號是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,且橢圓過點
,且橢圓過點![]()
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 在橢圓
在橢圓![]() 上,
上,![]() 是坐標原點,若
是坐標原點,若![]() ,判定四邊形
,判定四邊形![]() 的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】教材曾有介紹:圓![]() 上的點
上的點![]() 處的切線方程為
處的切線方程為![]() 。我們將其結論推廣:橢圓
。我們將其結論推廣:橢圓![]() 上的點
上的點![]() 處的切線方程為
處的切線方程為![]() ,在解本題時可以直接應用。已知,直線
,在解本題時可以直接應用。已知,直線![]() 與橢圓
與橢圓![]() 有且只有一個公共點.
有且只有一個公共點.
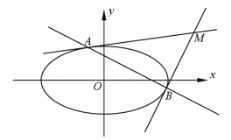
(1)求![]() 的值;
的值;
(2)設![]() 為坐標原點,過橢圓
為坐標原點,過橢圓![]() 上的兩點
上的兩點![]() 、
、![]() 分別作該橢圓的兩條切線
分別作該橢圓的兩條切線![]() 、
、![]() ,且
,且![]() 與
與![]() 交于點
交于點![]() 。當
。當![]() 變化時,求
變化時,求![]() 面積的最大值;
面積的最大值;
(3)在(2)的條件下,經過點![]() 作直線
作直線![]() 與該橢圓
與該橢圓![]() 交于
交于![]() 、
、![]() 兩點,在線段
兩點,在線段![]() 上存在點
上存在點![]() ,使
,使![]() 成立,試問:點
成立,試問:點![]() 是否在直線
是否在直線![]() 上,請說明理由.
上,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在改革開放40年成就展上某地區某農產品近幾年的產量統計表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
年產量(萬噸) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根據表中數據,建立![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() .
.
(2)根據線性回歸方程預測2020年該地區該農產品的年產量.
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線方程
,其回歸直線方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為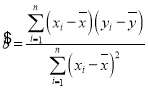 ,
,![]() .(參考數據:
.(參考數據:![]() ,計算結果保留到小數點后兩位)
,計算結果保留到小數點后兩位)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“互倒函數”的定義如下:對于定義域內每一個![]() ,都有
,都有![]() 成立,若現在已知函數
成立,若現在已知函數![]() 是定義域在
是定義域在![]() 的“互倒函數”,且當
的“互倒函數”,且當![]() 時,
時,![]() 成立.若函數
成立.若函數![]() (
(![]() )都恰有兩個不同的零點,則實數
)都恰有兩個不同的零點,則實數![]() 的取值范圍是( )
的取值范圍是( )
A.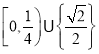 B.
B.![]() C.
C.![]() D.
D.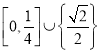
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com